お客を逃がさない釣り銭の用意の仕方
別の商業的課題を携えて相談に来る彼等に、その課題に沿って少数のデータで、手計算できるようにし、 その後、多量のデータの数学的処理をコンピュータでシミュレートして見せるスタイルで応えています。 彼等もそれに応え、事実データを収集してきてそれを分析し、意思決定に役立てようとしています。
- 手計算できる少数のデータで 問題：釣り銭として使える10円玉、５０円玉が計250円、10個の品物が入っている。この10個の品物 が売れる前に釣り銭が無くなって販売中止になる可能性を計算してみよう。 仮定：(1)50円の品物を売っている自販機とする。使用可能硬貨は10円玉、５０円玉、100円玉。 (2)100円を投入したときは、50円のお釣が出、お釣が無くなった時は販売中止のサインが出て 機械はストップする。また、客が50円玉以下の硬貨で品物を買った時は、それ以後お釣とし て使える仕組みになっている。 (3)客が100円玉一枚持って、品物を二つ買う場合は、まず100円玉で品物を一つ買い、50円の 釣り銭を受け取り、次の客が50円玉で買い物をしたと解釈して、常に客は一人の人が一つの 品物を買うと考える。
- 問題を「格子モデル」をシミュレータに（グラフ理論）グラフで考える
話は変わるが、確率計算にグラフが応用される例として、釣り銭の問題を考えてみよう。一般に商店では、開
店前にある程度の小銭を用意して釣り銭を用意するが、同じ商売を永年続けている場合は、経験的にどの程度の
小銭を揃えればよいか見当がつく。しかし、経験が役に立たないきもあるし、初めて商売する場合もある。その
ような場合に確率とグラフを用いて実験する方法を考えてみよう。
そこで、今はやりの自動販売機を用いて実際にこの問題を考察してみる。この自動販売機は50円の品物を売っ
ているとする、使える貨幣は硬貨のみで、十円玉、五十円玉、百円玉が使え、百円を投入したときは、五十円の
お釣りがでてくる。お釣りが無くなった時は発売中止のサインがでて、機械はストヅプする。お客が五十円以下
の硬貨、つまり、五十円玉一枚、または十円五枚で品物を買ったときは、その貨幣はそれ以後お釣りとしても使
えるような仕組みになっている。例題としてつぎのような場合を考える。五十円と十円の貨幣、つまりお釣りと
して使える硬貨計二百五十円、この自動販売機の中に残っていたとして、十個の品物が売れる前に釣り銭がなく
なって販売中止になる可能性を計算してみよう。
客が百円硬貨一枚持って、品物を二つ買う場合は、まず百円硬貨で品物を一つ買い、その釣りでもう一つの品
物を買うことになるが、このような場合は二人の客がきて、最初の客は百円もってきて、品物を一つ買い、五十
円の釣りを受け取り、つぎの客が五十円で買い物をしたことと解釈して、つねに客は一人の人が一つの品物を買
うと考えるのが普通である。
販売中止の時期
たまたま百円硬貨ばかり持った客が、つぎつぎと買いに来た場合には、二百五十円の釣りは、五人目の客でゼ
ロになり、そこで販売中止になってしまう。
また、最初に五十円で買い物に来た客があり、その後は全部百円玉しか持っていない客が来た場合を考えると、
最初に釣り用の小銭は二百五十円から三百円に増え、その後は五十円ずつ滅っていき、最初の客も入れて、七人
目の客が買い物をした後で、この自動販売機はストップする。これらの例で想像つくように、この問題を解く鍵
は客が百円玉を持ってくる確率と、五十円以下の硬貨を持ってくる確率如何と、何番目の客が五十円と百円硬貨
のどちらを持って買いに来たかによって定まる。このようなさまざまなケースを上手に分類する方法は、やはり
グラフを用いて、それぞれの場合の確率を計算するのが最高の手段である。
この自動販売機の釣り銭の状況を表すグラフはつぎのようになる。
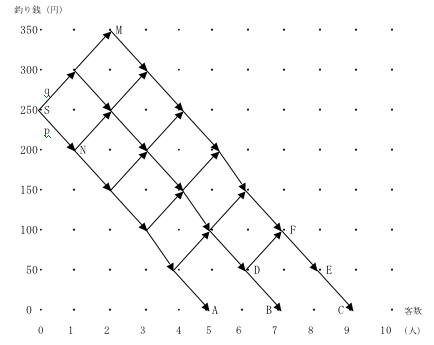x、y座標を使うと、x軸が何人目の人が買いに来たかを表し、y軸が釣り銭として使える小銭の金額を表す。
たとえば図の頂点、（5,200）は五人目の人が買いに来た後で釣り銭用の硬貨が二百円残っていることを示す。
矢印（有向辺）の意味
矢印には右上向きのものと右下向きのものがあるが、上向きの矢印はもちろん、客が五十円持て買いに来たの
で、釣り銭が五十円増加することを意味し、下向きの矢印は客が百円玉で買い物をしたために釣り銭用の貨幣が
五十円滅ることを意昧する。この図でわかるように、問題の自動販売機が販売中止となるときは、五人目の客か、
七人目のか、九人目の客が買いにきた後である。
五人目の客の後で販売中止になる場合は、五人の客のすぺてが百円玉を持って来た場合であ、七人目の客の後
で販売中止になる場合は、釣り銭なしの客が一人だけであり、九人目の場合は、釣り銭なしの客が二人だけの場
合である。
九人目の客が買いに来た後で、販売中止になる場合でも、釣り銭を必要としない二人の客が何番目に来たかに
よって、いろいろなケースに分かれ、それらのケースの数を数えあけないことには確率は求まらない。
販売中止の場合の数
それらのいろいろなケースは、それぞれこのグラフの一つずつの道によって表されている。ケースの数の数え
あげは、このグラフの道の数を計算することである。
道の数を計算する方法はバスカルの三角形による、二項係数の計算の方法と全く同じである。
パスカルの三角形は上図のような有向グラフであって、矢印によってつぎつぎと、二項係数に相当する頂点の値
を計算する方法である。ある頂点の値は、P から出発してその頂点に至る道の数であり、したがって、ある頂点
の値はその頂点へ向かって矢印が出ている頂点の値の和となる。
釣り銭のグラフの場合も、出発点Pから始まって、つぎつぎと頂点の値、すなわちその頂点に至るPからの道の
数を数えていくことができる。
以上から五人目、七人目、九人目の客が買いに来た後で釣り銭がゼロとなる場合の数は、それぞれ１、５、２０
であることがわかる。
販売中止の確率計算
一人の客が百円玉を持って買い物にくる確率と、五十円以下の硬貨を持って買いにくる確率をそれぞれP，qとす
る。もちろんP，qは p+q=1 (0＜p,q＜1)を満足していなければならない。十人目までの客が来る間に、釣り銭が
なくなって販売中止とる確率rは、r=p5＋5p6q＋20p7q2 で計算できることになる。
p、qの値は自動販売機の置かれる場所、時間、どんな硬貨を持って買いにくるかという客の種類等によって違
ってくるだろう。pの値が2/3,1/2,1/3の場合に試算してみると、それぞれ、 0.41 , 0.11 , 0.01となって、pの値
によって相当異なることがわかる。したがって、pの値をできるだけ正確に知ることが肝要である。
このように、このグラフはいろいろなケースを考えめぐらせ、それぞれの場合の確率計算を手計算するツールで
“格子モデル”とよんでいる。
その後、偽五百円硬貨悪用が流行って五百円硬貨を使えないようにした場合も考えるなど、高・大学生が「こん
な身近に数学があるのか」と感嘆する教材のひとつになっている。
- 数学的処理をコンピュータでシミュレートして見せる~多数データの場合~