- プ ロ ロ ー グ 「人当てマジック」に遊ぶ ＊＊＊＊＊［A］
画用紙大の数枚の紙に数人の顔の絵（以下、WANTED図。下の例では各３枚に４人）が貼っ
てあります。顔は下の「WANTED１〜３」図の通り、全部にあったり２枚や１枚だけにしかな
かったりします。
| WANTED１| WANTED２ | WANTED３ |
(上のWANTED１〜３からある人を覚えてもらい、一枚一枚にその人が居るか居ないかをマジシャ
ン役の私に知らせてもらいます。その情報だけから相手が覚えた人を私が当ててしまいます。
学び手（特に子どもの場合）の反応は「先生覚えているのでしょ」と冷ややか。そこで私はすか
さず同じように４枚８人の顔でも覚えてもらい、応答から素早く当ててしまう。すると、４枚８
人の場合まではとても覚えていられないと思う子どもたちは「エッ？！なんで分るの」、「不思
議だ〜！？」という反応に変わる。５枚１６人でもそれ以上でも原理は同じでどの子がどの顔を
覚えても必ず当てられる。
マジシャン役の私が言い当てたように、貴方がマジシャン役になって挑戦してみて下さい。
最初は、「３枚の画用紙大の紙に、人４人の顔写真」が載っているものから開始です（上の画
像をマウスでクリックすると大きな画像が見られます）。
できるかな？ また、４枚で、人数も多くなった８人のものにも挑戦してみて下さい。
さしあたって、マジックの種明かしをしますが、この程度の種明かしでは４枚８人の場合
にすら応用できません（別途、種明かししてあります）。
この種明かしではまだ本物ではありません。本物は、以降の 数学する(Do Math)ことから得
られます。
さあ いっしょに 「人当てマジックの不思議」を解き明かす 数学をしましょう！
- 現実問題に対処できる数学力養成を提起したOECD／PISA
２０００年からはじまったOECD／PISA調査『生きるための知識と技能』は、２００３年の
報告が２００４年１２月に公表されるに及んで、「成績順位の下落傾向が止まない」と報道・
教育界は大騒ぎした。しかし、日本が注目すべきデータは成績順位の上下という一過性の問題
でなく、学校数学が「数学への興味・関心・楽しみほか」を摘み取る営みを行いこの面で日本
の子どもたちが「際立って劣る」という国際診断が下されたことであり、また、PISA報告の
内容で評価すべきは、「知識やスキルが現実問題に活用できる形で習得されているか、すぐ使
える形で保持されているか、国の教育はそんな知識やスキルを育んできたか」という従来の知
識量でない基準による「教育の基調の転換」を問題開発と評価の指標を添えて提示したことで
ある。しかし、賛同できない点も幾つかある。その代表が国に問いかける形で、「そんな知識
やスキルを育んできたか」と教師に問いかけたものである。こう問いかけてるにもかかわらず
報告時点におけるPISAでは「どう育むかのプロセスなり技法の指導過程」については、問題開
発と評価の指標提示という性格上のためか、「関連のあるプロセスを理解することはまた、教
師が問題解決を指導する上で教育活動を準備できるようにする」 （ 『評価の枠組み』ｐ155）
という程度に止まっていた。
本稿テーマ名にはこう捉えPISAが世界の教育界に投げかけた基調、「問題解決能力の養成」
に一定の批判を込め、「それをどう育むか」の一案として冒頭の「人当てマジック」から開始
する３節以降を提起した。
この課題の核心は、学び手に「問題解決」能力はいかに醸成されると考え、どのような手
だてで実現できると考えるかにある。PISAは、開発した「現実問題からスタート」させ、巧
みに仕組んだ「解決プロセス」の回答分析でその能力を評価しようとするが、本稿では、学
び手を解決すべき課題と直面させ、持ち合わせの知識・経験を動員して深く考え結論づける
プロセスを体験させる。学び手が問題に直面し解こうとするのと、大人の作った与題を解く
違いは、リアリティのレベルにおいて学び手にとって決定的に異なる。
冒頭マジックの不思議さ(sense of wonder)から始まる、はじめは誰にも数学とは思わさ
ない不思議?発見の面白さ(sense of fun)は、幼児から大学生を含めた社会人までを同じス
タート台に立たせ探求心をくすぐる。
- 変装アイドルは誰だ？！
- 変装アイドル探し
ある人が銀行で変装して来店して
いたアイドル見かけた。他の目撃者
からつぎの情報が与えられている。
・眼鏡をかけていた
・帽子をかぶっていた
・首にネックレスやスカーフをしていた
・ペットを連れていた
そのアイドルは右の似顔絵の中に
いるというが、それはどの絵の人物
だろうか？
(この似顔絵はクリックすると拡大
印刷できます)
- 分類して解く ＊＊＊＊＊［A−1］
最も簡単な方法は、ハサミで絵をバラ
バラにし、目撃情報に沿ってあつまりの
分類・仲間あつめを行い該当者を割り出すやり方です。
（バラした絵は後でも使用します）
- 印をつけて見つける ＊＊＊＊＊［A−2］
先程の手法は小学入学生最初の算数教材に
あたる。しかし、残念ながら、これだけでは
冒頭「人当てマジック」の「謎解き」は難し
い。そこでこれを違ったもっと根拠のはっき
りした方法で考えよう。
人物絵の上に書いてある四つの○は、それ
は目撃情報に該当するかしないかの印をつけ
る（いま流行りの言葉で言えば ＜情報化す
る＞ と言う）ためのものです。
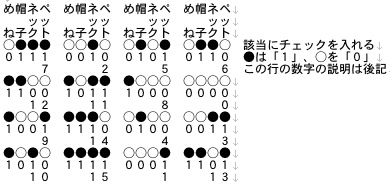
例えば、最上段左から３人目の人物は「帽
子をかぶり」、「ペットを連れている」ので
絵抜きの下表の該当する○を●に塗り潰す。
この例にならって全員の該当する○を●に
する。なお、４つの○の順番は絵の順番と同
じものとします。
変装アイドルにはどんな印が付くだろうか？
(似顔絵をクリックすると拡大印刷できます)
め 帽 ネ ペ｜め 帽 ネ ペ｜め 帽 ネ ペ｜め 帽 ネ ペ｜め 帽 ネ ペ
が ッ ッ｜が ッ ッ｜が ッ ッ｜が ッ ッ｜が ッ ッ
ね 子 ク ト｜ね 子 ク ト｜ね 子 ク ト｜ね 子 ク ト｜ね 子 ク ト
｜ ｜ ｜ ｜
○ ○ ○ ○｜○ ○ ○ ○｜○ ● ○ ●｜○ ○ ○ ○｜○ ○ ○ ○
○ ○ ○ ○｜○ ○ ○ ○｜○ ○ ○ ○｜○ ○ ○ ○｜○ ○ ○ ○
○ ○ ○ ○｜○ ○ ○ ○｜○ ○ ○ ○｜○ ○ ○ ○｜○ ○ ○ ○
○ ○ ○ ○｜○ ○ ○ ○｜○ ○ ○ ○｜○ ○ ○ ○｜○ ○ ○ ○
○ ○ ○ ○｜○ ○ ○ ○｜○ ○ ○ ○｜○ ○ ○ ○｜○ ○ ○ ○
- 変装アイドル探しを「数学する」
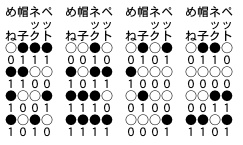
実は、○を０、●を１とすると、各顔は、１と０
の４桁の数字で表現できます。
○と●を書き込んだ絵の紙に、この４組の０と１も
書き込むと右表になる（似顔絵は省略した）。
- ２進法(the binary system)と
２進数 (a binary number)
＊＊＊＊＊［B-1］
４組の０と１で表現された数のことを4bit
の２進数という。
人間は、日常多くのことを10進数で表現す
る10進法を用いているが、○を０、●を１で
表わしたように、あらゆることを２進数で表
わそうとするのが２進法であり、他にもいろいろあります。
最も簡単なのが、電気回路のスイッチの「on/off」の説明で「オフ」の状態を表すの
を数字０、「オン」の状態を表すのを数字１で表すことや、硬貨の表/裏、真偽を示す
True/False の頭文字をとった T/F などもこの例にあたります。
基本的な２つの状態または状況にあり得るもの
ならば何でも、本来的に２進記数法に使えることを意味する。
- ２進数と10進数の双方向変換 ＊＊＊＊＊［B-２］
２進法や２進数の概念、その計算の理解などに、次のような格子のマス目と○●タ
イルを用いるとイメージしやすい。○●タイルは太めの孔空けポンチで工作紙や空き
箱などを打ち抜きその表裏を使う。
４bitの２進数なら横一列４マス□□□□。２進数づくりや計算はそのマスの中にタ
イルを置いて行う。例えば、左上図、●のある位の桁を「１」、空欄の桁を「０」
とすると２進数０００１である。 ＊＊＊＊＊［B-３］
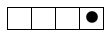左の２nは、２進数の位を表し、右から１位、２位、３位、４位。
右図のように、１位にもう一つ●を加えれば、一マス内に二つの
●が入るので繰り上げ２位に●を置き１位は空欄にして２進数
０ ０ ０ １ ０ ０１０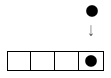
23 22 21 20 である（左下図参照）。
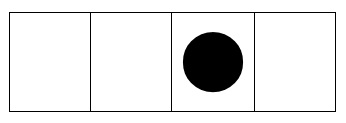10進数の「繰り上げ」と同じである。こうしてつぎつ
ぎと●を加え、繰り上げを行うと次々に2進数が作ら
０ ０ １ ０ れることになる。
この２進数を10進数に変換するには、２進数０１００を例にとれば
０×２3＋1×２2＋0×２1＋０×２0＝0×８＋1×４＋0×２＋０×１＝4
と計算すればいい。
計算でなくても、２進数０１００の２位が１になったならば２進数 ０１１０。
最初の２進数が１０進数４、これに２進数００１０つまり１０進数２が加わった
ので１０進数６と分る。
演習 HyperLink格子とタイルをclikして練習問題に答えよ。
演習の解は、上のHyper Linkをクリックすると、表計算ソフトが起動し、２進
数と10進数の交互変換のプロセスを学ぶことができます。２進法と２進数
問題１ 似顔絵の２進数を上記二つの方法で10進数に変換して書き込め。
（解は章末参照)
逆に、例えば、10進数３６を２進数に変換するには３６を２nで表すことを考えれ
ば、３６＝３２＋４より２5＋２2であるから下図の６マスの格子
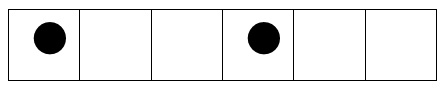図で●のある位を「１」、空欄の位を「０」とすると、2進数
１ ０ ０ １ ０ ０と表される。
２5 24 23 22 21 20
計算では次の通り。
１×２5＋０×２4＋０×２3＋１×２2＋０×２1＋０×２０＝１００１００
マス目を右図のように方眼状にすると2進数の四則計算をはじめ累乗、開平など
様々な計算ができる。
例題 ２進法による繰り上がりのあるかけ算 ３６×１９
３６を２進数で表す場合行下端に●タイルを３２と４に置く、１９の２進数は縦
に16と２と１の各行の３２と４の列の各交点にあたるマスに●タイルを置く。右端
「1＝2０」列以外のところにある●タイルをすべて図３の矢線のように斜め右上に
右端の「１＝2０」列に移動させる。すると６４の左マスには２つの●が入る。
この時は上記２進法の繰り上げの原則から上のマスに繰り上げて（図３の◎）２つ
の●はなくし空欄にする。
答えは「１＝2０」列の◎●タイルのあるマスを「１」、ないマスを「０」として下
から書いて２進数１０１０１０１１００。これを１０進数で表すには、◎●タイル
があるマスの右欄の１０進数4,8,32,128,512を加えればよく６８４である。
図 ３
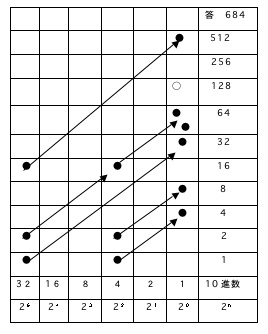もちろん前頁で行った計算をしてもよい。
なぜ、斜めに移動すれば良いのかを
（３２、１６）の交点Pで見ると
３２×１６＝２５×２４
＝２５＋４＝２９＝５１２
つまり、移動先は指数法則に則って
いるのである。
演習 残りの斜め右上に移動する
計算の指数法則の確かめを行え。
- 「人当てマジック」の
数学的「謎解き」
＊＊＊＊＊［C-1］
最後に、最初の“人当てマジッ
ク”の種明かしである。
図 ４
本稿冒頭の３枚のシートの各顔に
は１と０の４桁の数字で表現した
4bitの２進数と、これを10進数に変
換した10進数の２つの数字情報が書
き込めた。３枚のシートの各顔の裏
に顔に合わせて該当する１０進数を
書き込み、覚えた人がいると回答が
あった場合、各シートの裏面の最小
数字（「赤」丸囲んでおく）をすべ
て加えた数が覚えた人でこれを即座
に計算し当てる。
問題２１枚目だけにない、３枚目だ
けにない場合夫々について計算せよ。
解は章末参照
- 「人当てマジック」の不思議の種明かし ＊＊＊＊＊［C-2］
この最小数を加えれば、なぜ覚えた顔の数字になるのかの不思議が、学び手の前に立ちはだ
かる当面の関心事。果たしてその理由はなぜか？この理由を明らかにするために、新しい冒頭
のシート３枚に下表のように計算で顔の２進数と１０進数を書き込もう。まず、それぞれの最
小数を２進数で表わして、
１枚目の最小数4 0100 （このシートは帽子をかぶった人の集合）
２枚目の最小数2 0010 （このシートは首飾りをした人の集合）
３枚目の最小数1 0001 （このシートはペットを連れた人の集合）
２進数の最小数同士を加えて（括弧内は10進数）シートに書き込んでいくと、
図 ５
右表のように最小数を加え合わせることに
よって、各シートすべての顔の数字ができ
てしまう。そして共通な顔の数字になるの
は、当該カード同士の最小数を加え合わせ
たもののみで、他の数字は、異なる顔カー
ドを加えたときにできる数字である。
＊＊＊＊［D］
問題３ ３枚４人の「人当てマジック」
に倣って４枚８人のマジックがで
きるシートを自作せよ。
(解は章末参照)
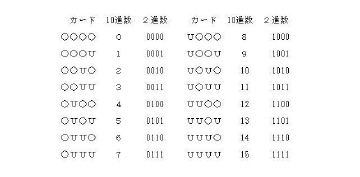
練習問題 下左図には10進数０から７まで（４、６除く）に対応する２進数が書いてある。
除いた４、６をまず、塗り潰し、下右図の10進数８から15までに対応する２進数カ
ードの略図を作れ。（左図のように該当する○を●に塗り潰せ。）
10進数 ２進数カード 10進数 ２進数カード
０ ○○○○ ８ ○○○○
１ ○○○● ９ ○○○○
２ ○○●○ 10 ○○○○
３ ○○●● 11 ○○○○
４ ○○○○ 12 ○○○○
５ ○●○● 13 ○○○○
６ ○○○○ 14 ○○○○
７ ○●●● 15 ○○○○
略図の解答
問題（「略図の解答」を参照に）回答に応じたマジシャン役の答え方を３枚４人の場合に倣って作って下さい。
演習 つぎに、2進数の四則計算をはじめとする様々な計算を考えてみましょう。
Excel起動後の第2sheetを出して下さい。
２進数の計算
練習問題）１枚目だけになかった、３枚目だけなかった夫々については、あなたが計算し
正解と照合して下さい。
上の例はごくありふれたものを挙げたが、およそ
基本的な２つの状態または状況にあり得るもの
ならば、何でも、本来的に２進記数法に使える。そこで２進用語的に身の回りを見渡す
と、思いもよらぬところにそれらを見ることができる。
まず、自然が断続するリズムを作るときはいつも２進数を作る・・・
波、一陣の風、雲間から顔を覗かせる日光。
また、人間活動は意識的あるいは無意識的に２進数列を作る・・・
ラジオから流れるロック・ミュージックは、オフビート・リズム、それは
トン〜バン〜トン〜バンという、２進数101(実際には、0101だが２進数
は0で始まらない）、ワルツはラ〜ダ〜ダと２進数100。
人工的システムでもそうです・・・
急行電車の停まる駅を１として数え、停まらない駅を0
として数えれば、これも２進数。灯台の灯の点/滅 etc.
- ２進法モデル２ 〜２進数 (a binary number ) カード〜
第７節では、上記の各種「基本的な２つの状態または状況にある」２進数の代表として、
シャッフルできるトランプのようなカードを作り、上端から１cm位の所にパンチで幾つかの
穴を開け、この穴の所々がＵ字型になるように上端から切り欠きを入れる。
切り欠き有り「１」、切り欠き無し「０」とし、２進法の応用や、２進数の計算、はたまた
アルゴリズムの分析にも利用することを例示する。
- 人はいかにして難問に対処してきたか
〜PISAの２つのプロセス〜 図 ６
１７世紀以来、文学界には戯曲『サー・トマス・
モアの本』は作者不明だがシェクスピアによるも
のかどうか？ が難問としてあった。
この文学界の難題に終止符をうつのにコンピュ
ータ駆使が熟した２０世紀後半まで待たねばなら
なかった。その経緯の概略が図６の流れ図で、左
上 A からはじまる右回り（B,C,D）のプロセスで
あった。
この難問解決において決定的な役割を果したの
はコンピュータ開発とその駆使であるが、それに
劣らず「文紋」採取という手法の開発は重要であ
る。なぜかというとこの手法はしかる後、日本で
も紫式部の『源氏物語』や日蓮上人の著作物にも
適用され、前者の５４巻中の後半１０巻は娘の作と認定、後者の真作は５０編中半分の２４編に過
ぎないと判定するのに用いられたように、それ独自が有用な方法だからである。(E)
「文紋」採取の手法の適用だけで難問の解決を図ったようなプロセスをPISAは（数学単独で解決
できる）「数学化プロセス」といい、多くの人々がこの難問解決に多様に関ったであろう３世紀に
渉る紆余曲折と、この上にコンピュータによって解決したアイディアの全体をPISAは、前者もその
一部とする領域横断的「問題に対処するプロセス」としている。
- 『生きるための知識と技能』としての数学力を育むために
数学活動においてもこの２つのプロセスの存在を語った数理科学者は少なくない。科学教育にも
提言の多いホワイトヘッドは『科学と近代世界』において次のように述べている(1981)。
次第に抽象的思考の領域に入り込んでゆく様子はまことに印象的、
数学はその上で、具体的事実の分析という重要な役割を果たすため
に地上に戻ってくる。・・・ここに、具体的なものを攻略するため
の武器が極度に抽象的であるという、パラドックスがある
図 ７
しかし、この２つのプロセスを内容とした教材プ
ランまでは数理科学者たちも詳しくは語らず、そ
の実現は教師たちの努力に待つほかない。
第４節までの本文中に A〜D と書き込んである
のは第５節に史実を使ってPISAの「問題解決プロ
セス」を紹介したステップ A〜D に対応する。同
じ流れ図にしたのが図７であるが、第４節までに
は、「文紋」採取の方法を例にした「数学化プロ
セス」(E)に対応するものがないことである。
それは第７節「紙製コンピュータを創る」全体が
該当する。
- 紙製の手づくりコンピュータ
ここでは引き続き「人当てマジック」を用いる。一組２５枚のカードを渡します。
このカードには４つの○の代わりに４
つの穴が空けてあります。いま黒丸を
上から切り欠きます。
(これをＵとしましょう)。
最上段左２番目の人物なら○ＵＵ○
となりますのでカードに「仲間集め」
で切り離した絵を貼付けます。同じよ
うに、カードに切り欠きを入れ、絵と
該当するカードを対応させ貼って下さい。
- カードで行う検索（サーチ）操作 ＊＊＊＊＊［Eー1］
カ−ドが仕上がったら、カードをシャ
ッフルし、配った爪楊枝を目撃者の情
報の第一であった“顔ホクロ”
の穴に差し込みカードを支えていた手
を放します。すると、顔ホクロの所が
切り欠かれていたカードが下に落ちま
す。犯人は落ちたカードの中にいるは
ずです。
同じく情報の第二から第四までの穴に
差し込んで落ちたカードの最後に犯人
が残ることになる。
このような操作をデータの検索（サーチ）という。
- カードで行う並べ替え（ソート）操作
＊＊＊＊＊［Eー2］
（１）カードをシャッフルし、順番を目茶苦茶にする。次に、爪楊枝を一番目の穴に差し
込みカードをもう一方の手の上にふるい落とす。落ちたカードの上に爪楊枝に残っている
カードを乗せ、爪楊枝を２番目の穴に差し込み同じ操作を行います。以下同様に３、４番
目の穴に差し込み篩い落とす作業を行うと、上から順番に番号を見ると小から大の順に並
らぶ。
この操作をデータの並び替え（ソート）と言います。
このソートがまた生徒たちにとっては「すんげ〜？！順番に並んでる」と歓声をおげ
る不思議なのです。
- ソートとサーチのアルゴリズム ＊＊＊＊＊［Eー3］
昇順ソートの不思議の仕組み（アルゴリズム）は以下の通りである。
カードをシャツフルして２進法でいう1の位２0の孔に爪楊枝をさして上に引っ張る。そ
うすると１の位が切り欠かれていない○、つまり「0」のもの(10進数でいえば0,2,4,6,…
…の偶数)が混ざった状態で検索(サーチ)されたことになる。そして爪楊枝に残った偶数
カードを元のカード（奇数）の上に置く（ここで偶数全体が奇数全体の上になった）。同
様にして右から2つ目２1の孔に爪楊枝をさして上に引っ張ると２進法でいう２の位が切り
欠かれていない○、つまり「0」のもの(10進数でいえば0,1,4,5,8……)が（偶数が奇数の
上にある）混ざった状態で爪楊枝に残る。そしてこの残ったカードを元のカードの上に置
く（ここで1が2の上に来る）。以下同様にしていくと、０はすべてに引っ掛かり、１５は
まったく引っ掛からないことから必然的に0のカードが一番上、１５のカードが一番下に
来る。その他の大小隣り合わせの２数は、１と２で見たように小さい数が大きい数の上に
並び替えられ、最終的には０から１５まで昇順に並べ替えられる。
演習 昇順ソートの理由を理解した上で、１５〜０の順番にカードが並ぶ
降順ソートの理由を書き、しかる後カードで行え。
サーチとソートは、コンピュータの基本動作であり、こうした意味から、このカードは
簡易コンピュータと言える。コンピュータが普及していなかった昔、カードによる検索と
並べ替えは図書館や学校、会社で使われていた。なお、現在主流のノイマン型コンピュー
タはこれに“記憶”装置を備えているわけです。
- 数学文化を問い直し、21世紀の早い時期に基調の転換を
第２節において、「現実問題からスタート」させその「解決プロセス」を分析して問題
解決能力を測るPISAの手法は、その問題も解決のプロセスも子どもたちにとってリアリティ
あるものとは言い難く適切でない、と批判し問題解決能力を育むプロセスの試みとして本
稿をスタートした。
「人当てマジック＆紙製コンピュータづくり」は、PISA２００３の遥か以前の１９５０
年代、「エンジニアの卵」であった私が、当時の数学・力学教育に欠けていると痛感した
「実際問題を数学化する」教育や「数学的アプローチがわからない諸現象に対処する」教
育を体験させる教材の工夫のひとつとして１９９０年代後半から実践してきたものである。
8-1. 具体と抽象間を上り下りする数学思考の体験を
私が、PISAに先駆けて、「学んだ以外の現実問題に対処できる」教育や「数学活動の知
的サイクルで構成する」学びなどを実践してきたのは、次のように要約できる数学（教育）
観に立っていたからである。
学び手の日常的対象に、動作や行動を知的に適用し、数学の論
理に導き、そうして獲得した、数学の諸形式を再び具体的事象
の解析に適用する
お気づきのように、これは第６節に引用したホワイトヘッドの数学観の教育版である。教
育版という意味は、ホワイトヘッドの「数学プロセス」は、人間の系統発生的な認識プロ
セスを指しているが、「教え＝学び」を主題とする教育においては、これに加えて個々の
子どもの個体発生的な認識プロセスの教材化が欠かせない。
この２つを固く結合した教材構成の原理として私はスローガンで、
具体世界と抽象世界の階段を上り下りする数学思考を育む
と言い。これをもう少し詳しくした双方向ダイアグラムで教材を構成してきた。
これがPISAと符合したわけである。しかし、これは私の独創ではない。なぜなら、教
育思想の歴史、例えば、ルソーやH.リードなどの「事物による教育」の系譜を知り、「構
成主義的スパイラル方式」が提起した子どもの表象構造の発達変容三段階説のプロセス
運動的表象 ⇒ 映像的表象 ⇒ 記号的表象
を知れば自ずと構想できることだからである。本稿中のプロセス記号と対応させれば次の
ようになる。運動的表象による認識段階（A）にある子どもが、ある対象物を運動的表象
によって認識した場合(A-1)、子どもが発達段階の経過とともに表象構造を変革しながら、
同一の対象物を映像的表象(A-2, A-3)、さらには記号的表象によって認識(B-1~C-2)する
ならば、その認識はより明確でより精確なものとなる（D）。こうしてブルーナーは「知
的活動は、学問の最前線であろうと、３年生の教室であろうと、どこにおいても同じであ
る」（『教育の過程』1961）と、科学的認識の思考・論理と学習者の学習・認識の論理の
同一性という結論を導き、この二つの違いは「程度(degree)」の事柄であって「質(kind)」
の問題ではないとした。
この方式は、その後、対話を重視する「社会的」構成主義と修正されたがここでは「双
方向」に修正した。これはホワイトヘッドの数学観をはじめ諸「数学活動のサイクル」説
を勘案すれば、プロセスEが位置づけられないその「単方向」性の限界はすぐ気付く。
- エピローグ
〜 学び手にとってリアリティある「知識とスキル」の教育を 〜
数学リテラシー、科学リテラシーを重視するPISAをスタンダードにする国が増え、我が
国でも頑な文科省も退潮著しい「読解力」を目の当りに方針転換をするなど徐々に影響が
見える。しかしPISAを生かすにあたって昭和４２年の文部省版数学教育「現代化」の失敗
の轍を踏んではならない。
本稿において、離散数学の一素材を例に、
学び手にとってリアリティある問題からスタートさせて、概念・手
法を開発し、その手法で問題を解き、最初の問題を解決する。しか
る後、別の異なる問題に解法を適用する
という一連のプロセスの実体験をしてもらったのは、未来の教師たちが、２１世紀の早い
時期に「知識やスキルを現実問題に対処できる力を育む」方向に日本の教育の基調の転換
を果す役割を担うにあたって視野に入れておくべきPISAの問題点と日本の数学教育の問題
点への警鐘と対案提示であった。
１）PISAを「現代化」の失敗当時のSMSGのように科学の体系・系統として過信しないこと。
「現代化」の失敗は、科学の体系・系統だけですべて解決すると、教科や教育内容の研究
の積み重ねによる教育的咀嚼を軽視した拙速がもたらしたもの。既存の科学の見地だけで、
あるいは数学の力量があれば数学教育は事足れりとする教科内容主義（仮称）の潮流はい
まだ根強い。その一方、現代の数学が果たしている役割に見合った適切な「現代化」作業
を怠り、旧態依然とした基礎・基本に固執する守旧的な数学教育もまた根強い。いずれの
潮流もPISAを適切に評価しえない。例えば、PISAを高評価できる中に、ブルーナーのいう
３年生よりは後にはなったが、１５歳青少年に自然・社会の現実問題を課し、解決プロセ
スを評価できるまでに問題開発したことが挙げられるが、従来の日本の学力論では大学教
育まで受けなければ与えられない類いの問題という先入観があった。
２）本稿でPISAに不足していると思われる教育独自の取り組みを補う方向を示す一方、我
が国の数学教育界にある潮流の下、現代の数学が果たしている役割に見合った教えるべき
基本（現代的な数学概念・方法）を明らかにし、その教育を短い期間に達成する子どもに
とってリアリティある「教え＝学び」のプロセス確立という新たな「現代化」作業を行う
必要を呼びかけた。この作業を疎かにした現在の数学教育の継続ではPISAも画餅に終わる。
これは各国の現行カリキュラムを不問に、「知識とスキルを現実問題に適用する」（OECD
-PISAプログラム責任者アンドレ・シュライシャー）ことだけに興味があるとするPISAのも
うひとつの問題点でもある。
３）子どもたちにとってリアリティある問題開発とは、生の自然・社会の問題だけでなく、
子どもたちの生活・文化を尊重した問題開発を意味する。
＜問題の略解＞
問題１
問題２ １枚目だけにないとは２、３枚目にあるという意。覚えてもらっ
た顔は各最小数の和２＋１＝３ よって３の顔の人。同様に、３枚目だけにないとは
１、２枚目にあること。従って４＋２＝６の顔の人。
問題３ ４枚８人の「人当てマジック」シート４枚の自作。
ペットと人の集合 {1,3,5,7,9,11,13,15}
ネック飾りの人の集合 {2,3,6,7,10,11,14,15}
帽子の人の集合 {4,5,6,7,12,13,14,15}
眼鏡の人の集合 {8,9,10,11,12,13,14,15}