���e�̊T�v
��ہE���ۊԂ̊K�i������~�肷�钊�ێv�l������Ώۂ�
�@�@�[�@�Q�[���E�N�C�Y�A���f���A�������w�@�[
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�R�݁@�����i�ΐ�j
�@�@�u����ꂪ�悭���ƌĂ�ł�����̂́A�����̟��𐰂炵��
�@�@��A�n�ӍH�v���ĂыN�������肷��p�Y���Ɏ��ۂ͂��߂��i�����j�B
�@�@�����̉Ȋw�i�����j�͍��{�I�ɂ̓p�Y���ł����Ȃ����̂ɑ����
�@�@��������Ă���i�����j���ʁA���퐶���Ɍ����鍢�f�����
�@�@��Ƃ�������ނ̖��i�����j�Ȋw�ł���|�p�ł���A���̂悤�Ȗ�
�@�@��ȏ�̂��̂Ɏ��g�ނ��Ƃ͂܂�ɂ��������Ȃ��v�i�j�X�y�b�g�j
�P�B�����͊w�Ԏ҂Ɏ��݊��E�����������������鋳�ނ���ŗǂ�
�@�����͎��݊��E����������f�Ђ���ł��A�W�J�A���_�͖{���I�ȔF���܂�
���ꂪ���́u�V�w���v�̂̊w�͊ρE���ފς����z���邽�߁v�̎��H������
����A������u���U�v��f�ނɕ���B
�@���E�����t�Ƃ̘b���𑍍�����ƁA�V�w�͊ς��E�߂̋��ނ́A�r���ۂ���
���u���쐫�{�y�����v�炵���B�Ƃ���ŁA�]������A�S���̍��Z���t�̑�
���ɂ͂`�l�h���̋��ނ̉B��t�@�����ĊO�����B�Ⴆ�A�O�ȓ��̋��ȏ���
���̋��ނ��A�����ł܂ݐH�����邪�A��͋��ȏ��ʂ�Ƃ����悤�ɂł���B
�`�l�h�̋��ނ�����A���̂悤�ȖڂƁu���쐫�{�y�����v���ފς͈ĊO�߂��A
�m�肷�邩�A�ے肷�邩�͕ʂƂ��āA�����Ă������咣�A�u�y������Ηǂ��v
��u���������̍m��v�̎w���v�̂ւ̈��̔��f�ƌ����Ȃ����Ȃ��B
�@���㉻�^���₩�肵���A���t�����́A����j�]�����������㉻�ɐU���
���ꂽ�ꂢ�o��������B���̓Q�܂Ȃ����߂ɂ��A�`�l�h�́A�V�w�͊ς�
���ފςɘf�킳��邱�Ƃ̂Ȃ����ނÂ���̕��r���N���ׂ����Ǝv���B
�X���I���G���e�[�����O�@
��Ֆڏ�̓��H�ɓ����̂���k�̓s�E�D�y�A�����ŊX���I���G���e�[��
���O�i�ȉ��A�P�ɃI���G���e�[�����O�Ƃ���j����i�@�@�j���̃N���X��
�s���v�悵���B
�@�y�\�z�z�I���G���e�[�����O�ɐ旧���āA�u�e�����_�����l�ʉ߂��邩��
�@�@�@�O�����ė\�z���Ăق����v�Ɩ��ꂽ��M���Ȃ�ǂ�����ł��傤���B
�@ ���̓�����ׂ����[���Ƃ���B
�@�@�@(1) ������H�ō��ƉE�̂ǂ���֍s������ׂɌ��߂�
�@�@(2) ����Ɍ������A�k�Ⓦ�ɋt�s���邱�Ƃ͂��Ȃ�
�@�@����ׂƂ́A�u�F�B���s�������玩�����s���v�Ƃ��A�u�������X������
�@�@�����炻����ɍs���v���Ƃ����̂ł͂Ȃ��A�Ⴆ�A�����_�Ŗ_��|��
�@�@�ē|�ꂽ���̓���I�ԂƂ��A�R�C���𓊂��A���̕\���ō��ɍs�����E��
�@�@�s���������߂邱�ƂȂǂ������B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�E�I���G���e�[�����O�̎���V�~�����[�^�[�@�[�@�i�@�q�@�[
�@�����ł͂S�O�l�̐��k�ŃI���G���e�[�����O���A�S�i�ڂ̊e�����_�����l
���ʉ߂��邩�Ƃ������Ƃ��l���邱�Ƃɂ���B
�@���̓I�ȎD�y�̒����݂ʒn�}�ɁA����ɕ��ʐ}������s�K�v�Ȃ��̂�
�̂Ăāi�̏ۂ���Ƃ����j�A�K�v�Ȍ�Ֆڏ�̓��H�Ԃ��������킷�Ɓu�i�q�v
��ɂȂ�i���ۂ���Ƃ����j�B��������f���ɁA�I���G���e�[�����O������
�ɍs��Ȃ��ŁA����Ŗ͋[�����E�V�~�����[�g�ł���B
���k�p�u���H�ԁv
�y���z��Ֆڏ�̓��H�ɓ����̂���k�̓s�E�D�y�A�����Ŏ��̃��[���ŊX��
�@�I���G���e�[�����O�i�ȉ��A�I���G���e�[�����O�j����i�@�@�j���̃N���X
�@���s���v�悵���B
�@�@�@(1) ������H�ō��ƉE�̂ǂ���֍s������ׂɌ��߂�
�@�@ (2) ����Ɍ������A�k�Ⓦ�ɋt�s���邱�Ƃ͂��Ȃ�
�@�@���̃I���G���e�[�����O�ɐ旧���āA�i�@�j�i�ڂ̊e�����_��ʉ߂���l
�@����O�����ė\�z���Ăق����B
�@�@�N�Ȃ�ǂ����@���v�������H
�@�u�F�B���s�������玩�����s���v�Ƃ��A�u�������X�����������炻����ɍs
���v�Ƃ����悤�Ȃ̂���ׂƂ����B�N�Ȃ疳��ׂɍs���H��I�Ԃ̂ɂǂ�ȕ�
�@�Ƃ�H
�@���̃N���X�̐l���́i�@�@�j���B�i�@�@�j�i�ڂ̊e�X�̌����_�����l�ʉ߂�
�邾�낤���H�@�ŏ��̌����_�̐l���͑S���ł��邱�Ƃ͒N�ɂł�������B����
���X�^�[�g�����i�ڂ̓�̌����_�ł͔��X���낤���H
�@�\�z�𗧂Ă�ɂ͂ǂ�����������Ƃ����ƁA���̂悤�Ȑ��w�I���ۂ̍l
�����ŃI���G���e�[�����O�����ۂɍs��Ȃ��Ă�����łł���B
�@�����͋[�����i�V�~�����[�g�j�Ƃ����B
�@�@�@�@�@�@�@�@�@�@�@�@��
�@�@�@�@�@�@�@�@�@�@�̏ہ�
��
��
���̏�
��

��
�@�@ �����_��������
��
�@�@�@�@�@�@�@�@�@�@�@�@
�y��������z�����_�n���X�^�[�g�ɁA�P���̃R�C���𓊂��āA�\�Ȃ�i������
�āj�E�i�݁A���Ȃ獶�i�ރI���G���e�[�����O���i�q��Ŏ��{���ĉ������B
�܂��\���u�P�v�A�����u�O�v�Ƃ��Ă��̕\���̏o���𖼕\���ɍ����ɋL�^����
�������B���ɁA�e�l���i�q�Ŗ͋[�����������ʂ����\�ɏW�v���ĉ������B�j�i
�ڂ̌����_�̕����ɂ́A�����̒ʂ��������Ɋۈ��ł��A��i�ڂ̊��ʂɂ͏W
�v�����ꍇ�̗\�z�l�����L�����ĉ������B�O�i�ڂőS���̏W�v������ƁA�e��
���_��ʂ����l���������邱�ƂɂȂ�A�\�z�̓��ۂ������邱�ƂɂȂ�܂��B
�@�@�@�\�z�l���@�@�@ ( �@) (�@ ) (�@ ) ( �@)�@( �@)
�@�@�@�� �� �_�@ �@�i�@�@�j�@�@�k�@�@�l�@�@�m
�@�@�@�S�̏W�v �@�@ ( �@)�@(�@ ) (�@ )�@( �@)�@( �@)
�@�L�^���\�́@�L�����S���̋L�^���W�v���܂��B
�@�Ⴆ�A�X�^�[�g���Ă���S�i�ڂ̌����_�̂ǂ���ʂ邩�ׂ�ꍇ�A�S
�Ԗڂ܂ł̐���Œʂ�����_��������B�@�@�@
�@���̎���V�~�����[�g�̃f�[�^����S���k���ǂ̌����_��ʂ邩�\�z�𗧂�
��Ƃ��A�����̒ʂ�����_�����߂邾���̂S�i�ڂ܂ł̃f�[�^�ł͗\�z�͂�
�܂�������𑱂��ĉ������B
�@�e�l�R�S�C�̐��ʂ̕������

�@�@�ʂ����ăl�R���̐��_�͐��������B�ނ̌��������`�G�b�N���Ă݂悤�B
�@�y�\�z�z�e�l�R�S�C�̐��ʂ̕ʂ���ɑ���M���̗\�z���A���̑I������
�@�@�@�@���I�ѕ����ɁZ���ł��ĉ������B���ʂ̓N���X�W�v�Ɏg����
�@�@�@�@�ŋL�����Ȃ����ƁB�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�A�D�S�������@�C�D�R�P�@�E�D�Q�Q�@
�@�@�@�@�N���X�W�v���@�@�i�@�@�@�j �@�i�@�@�@�j�@�i�@�@�@�j
�@���̎��Ə��́A�m���̃p���h�b�N�X�u�l�R�Ƃ̐l�X�v�i�l�D�K�\�h�i�j���璅�z
���B
�@���Ƃł͐��k�ɂ���������ʂ薟�����ŗ^����B����ƁA�u�N���A�S�l�Z
��̐l���Ȃ��H�v�u���̒m���Ă���S�l�Z��̉ƒ�͂R�P���v�u���⎄�̒m
���Ă���Ƃ͂Q�Q���v�ȂǂƂS�l�̎q��������l�Ԃ̉ƒ�̏������W����
���B
�@�����đI��������I��ʼn���B������W�v����ƁA�ǂ̃N���X�ł��S��
�����͈�ԏ��Ȃ����A�R�P�ƂQ�Q�̓N���X���̏������ɂ��e������Ă�
���炩�������Ȃ�B�@�@�@�@�@�@�@�@�@
�@�I���G���e�[�����O�ŁA�D�y�̌�Ֆڏ�̒����݂��u�i�q�v�ɒ��ۂ��čl��
���̂Ɠ������A���̖��́A�S���̃R�C�������f���ɂ���ƁA�l�Ԃ̉ƒ�̂S
�l�̎q���̐��ʂ̕�����A�Ƃ����W�c�i��ʁj���R���ۂ��茳�ł��₷���Č�
�ł�������ɒ��ۉ��ł���B
�Q�B�y���Ƃ��{���I�F���ɂȂ���Q�[���@�[���ۉ��̃v���Z�X��������[
�y��������z�����_�n���X�^�[�g�ɁA�P���̃R�C���𓊂��āA�\�Ȃ�i�F����
�@���猩�āj�E�i�݁A���Ȃ獶�i�ރI���G���e�[�����O���i�q��Ŏ��{��
�@��B�܂��\���u�P�v�A�����u�O�v�Ƃ��āA���̕\���̏o����ʎ����\���ɍ�
�@���ɋL�^����B
�@�@���ɁA�e�l���i�q�Ŗ͋[�����������ʂ����\�ɏW�v����B�j�i�ڂ̌����_
�@�̕����̎����̒ʂ��������Ɋۈ��ł��A��i�ڂ̊��ʂɃR�C���𓊂�����
�@�G����S�������W�v�����ꍇ�̗\�z�l�����L������B�O�i�ڂőS���̏W�v��
�@����Ɗe�����_��ʂ�l���������邱�ƂɂȂ�A�\�z�̓��ۂ������邱�Ƃ�
�@�Ȃ�B�L�^���\�͉L�����S���̋L�^���W�v������̂Ƃ���B
�@�@�@�\�z�l���@�@�@�@�@ ( �@)(�@ )(�@ )( �@)( �@)
�@�@�@�� �� �_�@ �@�i�@�@�j�@�@�k�@�@�l�@�@�m
�@�@�@�S�̏W�v �@�@�@�@�@ ( �@)(�@ )(�@ )( �@)( �@)
�@�F����������_�n�ɗ����āA�R�C���𓊂��Ȃ���\�Ȃ�i�F���猩�āj
�E�ɐi�݁A�P�ƋL�^���A���Ȃ獶�ɐi�݁A�O�ƋL�^���Ȃ���I���G���e�[����
�O���Ē��������B����ƁA���̓�l�̐��k�̋L�^�̂悤�ȂO�ƂP�̐��ł�
��͂����B�������A����͂S�O�����_��ʉ߂����L�^�ł���B
�@�@�@�@�O�O�P�O�O�O�O�P�O�P�@�@�@�@�@�@�@�@�P�P�O�P�P�O�O�O�P�O�@
�@�@�@�@�P�O�P�O�O�P�O�O�P�P�@�@�@�@�@�@�@�@�O�P�O�P�P�P�O�P�O�O
�@�@�@�@�P�P�O�O�P�O�P�P�P�P�@�@�@�@�@�@�@�@�O�O�P�P�O�P�O�P�P�O
�@�@�@�@�P�O�O�O�P�O�P�O�P�P�@�@�@�@�@�@�@�@�O�O�O�P�P�O�P�O�O�O
�@�O�ƂP�̕��т̃p�^�[���������p�^�[���ɂȂ邱�Ƃ͂܂��Ȃ��̂ŁA�P�N��
�X�̐l�����̃p�^�[�����ł��邱�ƂɂȂ�B
�@�����̐��k�͌����_�k���A�E���̐��k�͌����_�j��ʂ邱�ƂɂȂ�܂�����
���ꂼ��̐��k�͂k�C�j�Ɋۈ��ł��ƂɂȂ�܂��B
�@���k�͂��̎���V�~�����[�g����A�e�����_�̗\�z�𗧂Ă邱�ƂɂȂ�܂��B
�����ł���l�̐��k�̗\�z�������Ă����܂��傤�B�������A���k���S�O���Ƃ�
���Ƃ���\�z���Ă�������B
�@�@�@�� �� �_ �@�i�@�@�j�@�@�k�@�@�l�@�@�m
�@�@�@�\�z�l���@�@�@�@ (�P�j (10) (15) (10) (�R)
�@�@�@�\�z�l�� �@�@�@ (�Q)�@(�X)�@(15) (10) (�R)
�@�Q�N���X�ŏW�v��������V�~�����[�g�̌��ʂ͎��̒ʂ�ł���B
�@�@�@�� �� �_ �@�i�@�@�j�@�@�k�@�@�l�@�@�m
�@�@�@�S�̏W�v �@�@�@ (�O�j (10) (17) (�X) (�P)�E�E�E�R�V���N���X
�@�@�@�S�̏W�v�@�@�@ (�P)�@(11)�@(13) (11) (�Q)�E�E�E�R�W���N���X
�@�Ȃ�Ɨ\�z���߂����Ƃł��傤�B���w�I�Ɍv�Z���邱�ƂɂȂ邱�̌オ����
�ÁX�Ƃ������ƂɂȂ�܂��B
�y�S���̃R�C�������̎����z�S�l�̐��ʂ̕�������̂悤�ɂ���Ǝ����ł���B
�@�@�S�l�̎q���̂����@�@�@�@�@�@�@�@�E�E�E�E�S���̃R�C���𓊂���
�@�@�Y�������A��ʂɂ͒j�������̂����E�E�E�E�\���̕��������
�@�@�Ƒ����̂����@�@�@�@�@�@�@�@�@�@�E�E�E�E����������Ē��ׂ�B
�@�����ł́A40��S���̃R�C�����ɓ����āA�\�����̕���������L�^����
���B�������A�L�^���鎞�͕\���o��P�A�����o��O�ƕ\�킷���̂Ƃ���B
�@�@���ʂ̕�����̏W�v�@�@�S�������@�Q�F�Q�@�R�F�P�@�@�@�@
�@�i�@�@�j�ǁ@�@�@�@�@�@ �i �j�@ �i �j�@�i �j
�@�@�e�̋L�^�@�@�@�@�@�@�P�@�@�Q�@�@�R�@�@�S
�@�F������A���ۂɁA�S���̃R�C���𓊂��Ď������L�^���Ē��������B������
���I���G���e�[�����O�̂Ƃ��Ɠ������A���k�����i�Q����g�j�̎����f�[�^��
�P�N���X�����������B
�@��No.�@�@�@�P �Q �R �S �T �U �V �W �X 10 11 12 13 14 15 16 �v�@�䗦
�S�������@�@ �W �T �Q �R �X �V �V �R �T �U �V �T �R �T �U �Q�@89�@0.125
�R�F�P�@�@�@ 19 19 23 21 21 18 20 21 17 18 13 24 21 19 22 29 343 0.5
�Q�F�Q 13 16 15 16 10 15 13 16 18 16 20 11 16 16 12 �X 248 0.355
�@�@�@�@ 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 680
������R�C���Ŏ��������f�[�^�̍��v�����߁A�䗦���v�Z���邱�Ƃ́A�{��
�Ȃ�ΐ������͂Ȃ����A����̊m���v�Z�̎Q�l�܂łɍ��v���A�䗦���o���Ă�
���B
�R�B�x���k�[�C���z�E���s�Ɠ��z�@�[���ۉ��̃v���Z�X��������Q�[
�@�I���G���e�[�����O�́A����̌����_�ŁA���E�ɕ�����镪�������S��
�̃R�C��������������A�\���̕������������Ƃ��A����ɂP�A�����ɂO��^
����i�R�[�h���Ƃ����j�ƁA�m�����z�̒��ōł���{�I�ȃx���k�[�C���z����
���v�I�u���U�v�ϐ��邱�ƂɂȂ�B
�@���̊m�����z�ɑΉ��Â������͂�����ł�����B�Q�[���̏��s�A�\�z�I
���̐��ہA���f�̓��ۂȂǁA���̌��ʂ̂Q�ʂ�̎��ۂ��O�A�P�̕ϐ��ŕ\�킹
�A���̕��z�̌`�ɂȂ�B���̂Ƃ�����̎��ۂ��u�����v�ƌĂԂ��Ƃ�����B
���̕��z���Ȃ��m�������̓x���k�[�C���s�Ɩ��Â����A�m�����f���̋c�_��
�Ȃ��ł��d�v�Ȃ��̂ł���B
�@������̎��s�ŁA����������P�A���s������O��^�����Ƃ��̃x���k�[�C��
�z����m�����z�A�Ⴆ�A�R�C�������̎����ŁA�����̍d�݁A���邢�͂P����
�������Ƃ��A�\�ɂȂ閇�����m���ϐ��Ɍ����Ă�ƁA����͂O�A�P�A�Q�A
�E�E�E���ƁA�O����͂��܂��ăR�C���̖����܂ł� n�{1 �ʂ�̐����l���Ƃ�B
�@���̂悤�Ƀx���k�[�C���s������g�Ƃ����Ƃ��A�w�肳�ꂽ���ʂ̐�
�N������m���ϐ��Ƃ����m�����z���u���z�v�ƌĂ�ł���B
�@���́u�I���G���e�[�����O�v�Ɓu�S���̃R�C�������v�ɂ͂��悤�ȋ��ʓ_
������B
�@(1) �N���肤�錋�ʂ���ʂ�Ɏ}�����ꂷ��B
�@(2) ���̓��ɐ܂��m����R�C���̕\�̏o��m�����^�����Ă��āA���̒l�A
�@�@���ǂ̎��_�ł��ς��Ȃ��B
�@(3) ����������ƌĂ����̂ŁA�I���G���e�[�����O�̏ꍇ�A�e�X��
�@�@��̌����_�ō����E���ɕ�����閈�Ɉ��̎������s��ꂽ�ƍl���āA
�@�@�S�i�ڂ̌����_�͎����S�Ɖ��߂���B�S���̃R�C�������̏ꍇ�A�\��
�@�@�����Ƃ����}������𑱂��Ċώ@�����i�S��������S�j�ł���B
�@���̓���A���̋��ʂ��Ă���m���I�ȓ����ɒ��ڂ��āA�������S�A�m
���̒l�� 0.5�̓��z�ɂ���Đ����ł���u�����v�Ƃ����B
�E�X���I���G���e�[�����O���u���w����v
�@�I���G���e�[�����O�̎���V�~�����[�g�͈ȉ��̂悤�ɍl����ƁA�i�q���
�̃I���G���e�[�����O����s��Ȃ��Ă��\���ł���B
�@�܂��A�D�y�w�ɍ~�藧���w�O�̌����_�n�ɍs���H�͂P�����Ȃ��̂ŁA�I��
�̗]�n�͂Ȃ��P�ʂ�B�͂��߂̌����_�n����͂Q�̘H�̂ǂ��炩��I�Ȃ�
��Ȃ�Ȃ��Ȃ�A����̘H�ɓ��邩�A�E��̘H�ɓ��邩�̂ǂ��炩�ŁA����
��̉\�����P�A�P�Ə����B���̌���
�_�b�A�c�A�d�ɗ���ƁA����܂ō��̘H �P ����
��I�҂��������̘H�ɁA����܂ʼnE �P �P �P�i��
�̘H��I�҂������E�̘H�ɓ��邱�� �P �Q �P �Q�i��
���ł��A���̉\���͂��ꂼ��P�B���� ( ) ( ) ( ) ( ) �R�i��
�_�a�ɓ���ɂ͂Q�̉\��������A�� ( ) ( )( )( ) ( ) �S�i��
���ɍ���I�l�����x�͉E�ƑI�Ԃ��A
���邢�͍ŏ��ɉE��I�l�����x�͍���I�Ԃ��̂Q������A���̌����_��
�̉\�����P�A�Q�A�P�Ə����B���̐���́A�����_�b�A�c�A�d�ɁA���ꂼ�ꉽ
��ނ̘H��ʂ��ē��B�ł��邩�������Ă���Ɠ����ɁA�����_��ʂ鐶�k�̐l
������\�킷�B�܂��A�@���̂Q�i�ڂ̉\���̑����́A�P�{�Q�{�P���S���Q2
�ƕ\�킹�邪�A����͓����̐����Ӗ�����B
�@���P�j�S�i�ڂ̌����_�i�A�j�A�k�A�l�A�m�ɑ��邷�ׂẲ\���𐔗�
�@�@�@�@�ŕ\�킷�Ƃǂ��Ȃ邩�B�܂��A���̉\���̑����������B
�@�@�@�Q�j10�i�ڂ̌����_�ɑ��邷�ׂẲ\���̐���͂ǂ��Ȃ邾�낤���B
�@�@�@�@�܂��\���̑����͂ǂ��\���ł��邩�B�������A�T�A�U�A�V�i�ڂƏ�
�@�@�@�@�ɋ��߂�̂ł͂Ȃ��S�i�ڂ܂ł̐���\�z���ĉ������B
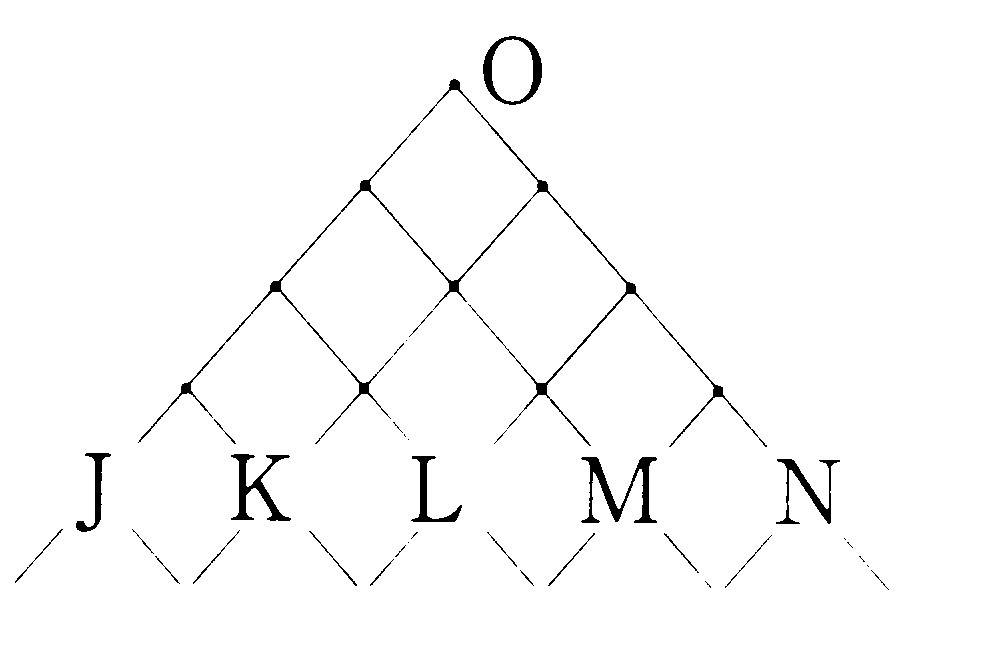
�@�����_�i��ʉ߂���l���̓p�X�J���̎O�p�`�̍ŏ�����S�i�ڂ܂ł̍��[��
�ʂ鎞���Ӗ����邩��A�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�P�~(0.5)�~(0.5)�~(0.5)�~(0.5)��6.25���@�@
�@�l���͎Q����40��������@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�n
�@�@6.25�~40��100��2.5�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �`�@�@�a
�Q�A�R�����Ӗ�����B�@ �@�b�@ �c�@�@�d
�@�j��ʉ߂���l�̔䗦�����߂�ɂ́A�e�@�@�@�@ �e �f�@�@�g �@�h�@
�i�̌����_�� �i �j�@ �k�@�@�l�@�m�@
�@�@(�)�@���E���E���E�E
�@�@(�)�@���E���E�E�E�� �����_�̕t��
�@�@(�)�@���E�E�E���E��
�@�@(�)�@�E�E���E���E��
�Ƃ����ǂꂩ��̌o�H�����ǂ�Ȃ���Ȃ�Ȃ�����A�Ⴆ�� (�)�̌o�H����
�ǂ�m���́A���E�̕�������̊m�������� 0.5�Ȃ̂ŁA�i�Ɠ��l6.25���B����
�O�̌o�H�ɂ��Ă������l�ɂȂ邩��A���Nj��߂�䗦�́A
�@ �@6.25���~�S��25��
�̂悤�ɋ��߂�A���l�ɐl���v�Z����ƂP�O���ł���B
�@�c��O�̌����_�̏ꍇ�������l�ɋ��߂��
�@�@(�i)�@�P�~(0.5)4 �@�@ �@�� 6.25���@�@�l���Q�A�R��
�@�@(�j)�@�S�~(0.5)3�~(0.5)1 ��25 ���@�@�l���P�O��
�@�@(�k)�@�U�~(0.5)2 �~(0.5)2 ��37.5 ���@�@�l���P�T��
�@�@(�l)�@�S�~(0.5)1�~(0.5)3 ��24 ���@�@�l���P�O��
�@�@(�m)�@�P�~�@�@�@�@ (0.5)4 �� 6.25���@�@�l���Q�A�R��
�E�S���̃R�C�������̎������u���w����v
�S���̃R�C�������̎����ł́A�N���肤�錋�ʂ͉��L�̒ʂ�ŁA��̐�����
�R�C���ԍ��A���[�͌��ʂ̃J�E���g���őS���łP�U�ʂ肠��B�������\�̖���
������Ƃ������ʂł݂�A�O����S���܂ł̂T�ʂ肵���Ȃ��B
�@�e�P�[�X�̋N���肤��m���̒l�́A�E�[�̗�Ɏ������B
�@ �P�Q�R�S�@�@�\�̐��@�@�@�@�@�@�@�m�@��
1 �P�P�P�P�@�@�@�S�@�@�@�P�~(0.5)4�@�@ �@ �� 6.25��
2 �P�P�P�O�@�@�@�R�@�@�@�S�~(0.5)3�~(0.5)1 ��25 ��
3 �P�P�O�P�@
4 �P�O�P�P�@
5 �O�P�P�P�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
6 �P�P�O�O�@�@�@�Q�@�@�@�U�~(0.5)2�~(0.5)2 ��37.5 ��
7 �P�O�P�O
8 �O�P�P�O
9 �P�O�O�P
10 �O�P�O�P
11 �O�O�P�P
12 �P�O�O�O�@�@�@�P�@�@�@�S�~(0.5)3�~(0.5)1 ��25 ��
13 �O�P�O�O
14 �O�O�P�O
15 �O�O�O�P
16 �O�O�O�O�@�@�@�O�@�@�@�P�~�@�@�@�@(0.5)4 �� 6.25���@
�S�����ׂĂ��u�\�v�Ƃ����̂́A�����_�m�̒ʉ߂��l����̂Ɠ����ł���A�R
�����u�\�v�Ƃ͌����_�l�̒ʉ߂��l���邱�ƂƓ����ł���B
�S�B���w�̒��ی`������̉����čl����Ƃ�������
�@�@�u���鐔�w�I�w�₪�o���I���牓������ɂ�āA�܂��Ă��ꂪ
�@�@�w�����x���琶�܂ꂽ�z�O�̑������Ԑڂɂ����Ȃ���Q��A��R
�@�@��̂��̂ɂȂ��Ă���ƁA���̎��ӂɂ͏d��Ȋ댯���܂Ƃ����B
�@�@�i�����j��x���̒i�K�ɒB����ƁA�E�E���̎��Â̕��@�͌���ɗ���
�@�@�Ԃ��āE�E�o���I�z�O���Ȃ菬�Ȃ蒼�ڂɍĒ������邱�ƁA�����
�@�@�O�ɂ͂Ȃ��悤�Ɏv����v�i�m�C�}���j
�@�`�l�h���w�Z���H�ɂ́A�V�F�[�}��}��́u�ʂ���̒��ہv�ƁA�Z���`����
�u���Â���v������Ƃ��������ꂽ�~�ς����邪�A���w�E���Z�ł͏��Ȃ���
���Ă��܂��B���ې����[�܂��ē���Ȃ邽�߂��낤���A���ɁA���ی`������
�̎���Ɍ��т����҂��r�������B�@�@�@�@�@�@�@�@�@�@�@�@
�@�{���|�[�g�ŁA�X���݂��瓹�H�ԈȊO�̕s�K�v�ȕ����̏ۂ��A�u���ہv����
���i�q���g���Ďv�l�����炵�A���w�`���ɓ��点�A�S�l�̎q���̐��ʂ̕�����
���R�C�������Ɂu���f���v�����A����������A����ɂ́A���̗��҂̐��w�I�\
���������Ƃ������Ƃ�ʂ��āu���w�v�����铙�̃v���Z�X��厖�ɂ����̂́A
���ۉ��Ƃ��̐[�܂肻�̂��̂�������Ώۂɂ�������ł���B
�@���̌ʂ̑ΏۂƁA���w�`���Ƃ�}�����̂Ƃ��čl���o�����A����̕�
�ł�����A�����ە��ł�����A�i�q�Ȃ�R�C���Ȃ�́A�ŏ��̌ʂ̋�̐���
�������āA���ۓI�\���������o���I�E���ۓI�����u���w�v������c�[���Ƃ�
�Ă̖������ʂ�������ŁA���ۓI�E��ʓI�Ȑ��w�`�����i�q�Ȃ�R�C���Ȃ��
�ʂ��āA���̋�̂��C���[�W�����邱�Ƃ��ł��邱�Ƃ��Ӗ�����B
�@�����āA���̌�҂̑��ʂ����A�}�E���E�v�Z�����̓I�C���\�W��D���A�l
�𐔊w�̑O�ŗ���␂܂��Ă����A���ۉ��ƈ�ʉ�������Ƃ���u���w�v������
���ΏۂɁA�v�l�ƈӖ��������Ă������̂ɂق��Ȃ�Ȃ��B
�@���ȏ���Q�l���ɂ��邳�����듊����R�C�������A�����̖��Ȃǂɂ͂���
���_�͂Ȃ��A�P�Ȃ���K���̈�Ɉʒu�Â����Ă���ɉ߂��Ȃ��B
�@�����ł́A���w�̖����u�i�q�v�ɋ�̉����邱�Ƃɂ���āA�v�l�����炵�A
�Ӗ��������Ƃ����A���w����Ɏv�l�ƈӖ��������Ƃ��ċ����悤�B
�@�u�����{���̂S��̓W�J���̊e���̌W���͂ǂ�Ȓl���v�Ƃ������w�̖�
����ɂƂ낤�B�@
�@�u�i�q�v�Ƃ��A���̓��͂ǂ��֘A����̂��Ƃ����ƁB
�@�����_�ō��ɍs�����Ƃ����A�E�ɍs�����Ƃ����Ƃ��A�e�����_�ł̕������
�}������Ɖ��}���̂悤�ɂȂ�B���{���̎����͎}���ꂷ����Ӗ������
�ŁA�X�^�[�g�O�͂O��A�X�^�[�g���ĂP��A���̌����_��ʉ߂��ĂQ��Ƃ���
�悤�ɂł���B���������Ď��}�̂悤�ɕ\���邱�ƂɂȂ�B
�@�@�@�@�@�@ �P�@�@�@�@ �E�E�E(���{��)0
�@�@�@�@�@ �� ���@�@�@ �E�E�E(���{��)1
�@ �� ���� ���@ �E�E�E(���{��)2
�@�� ���� ���� �� �E�E�E(���{��)3
�@�� ���� ���� ���� �� �E�E�E(���{��)4
�@����ł͓W�J���͂ǂ��������Ƃ��Ӗ�����̂��낤�B�Q��̓W�J��
��2�{2�����{��2��\���}���ꂪ�ǂ������Ӗ����������l����Ε�����B
�@�X�^�[�g���獶���Ɛi�ނƂP�~���~���܂肘2�B�X�^�[�g���獶�E�ƉE��
�Ɛi�ނƂ����Ƃ����B�E�E����2 ���Ӗ�����B���̘a�ł���W�J���́A����
�̂Ƃ��Ɠ������}������̉i�p�x�j���Ӗ����Ă���B
�@�������āA���{���̂S��̓W�J���̊e���̌W�������߂邱�ƂƃI���G���e�[
�����O�̂S�i�ڂ̌����_�ɑ��邷�ׂẲ\���̐�������߂邱�Ƃ͓�����
��ł���A���������āA���}�̂悤�ɁA���̗ݏ�v�Z�̊e���̌W���ƃp�X
�J���̎O�p�`�̐��w�I���炭�肪�����ł��邱�Ƃ�������B
�@�@�@�@�@�@(���{��)0���@�@�@ �P�� �P
�@�@�@�@�@�@(���{��)1���@�@ ���{�� �P �P
�@�@�@�@�@�@(���{��)2�� ��2+2����+��2 �P �Q �P
�@�@�@�@�@�@(���{��)3����3+3��2��+3����2+��3 �P �R �R �@�P
�@�@�@
�@�@�@�@�@�@�@�@�@���̓W�J�@�@�@�@�@�@�@�@�@�p�X�J���̎O�p�`
�T�B���U�I�m�����z����A���I�m�����z�ց[�@��ʉ��Ɗg���@�[�@
�@�u�U�l����S�l�̖�����I�ԕ��@�͉��ʂ�H�v�A�u���꒼����ɂȂ��U�_��
�S�_������łł���l�p�`�͉��ʂ�H�v�Ȃǂ́A�g�����_�̏����I���ň��
�I�ɂ́u�قȂ�U����S�Ƃ�g�����͉��ʂ�H�v�Ƃ������ƂɂȂ�B
�@�������
�@�@�@6�b4���i�U�~�T�~�S�~�R�j�^�i�S�~�R�~�Q�~�P�j��15
�ƌv�Z����B���̐��w�L��6�b4�̂b�͑g�����̉p��combination�̓���������
�������́B
�@���̑g���� 6�b4���܂��A�S���̃R�C�������̎����̐��w�I���炭�肪�A�I��
�G���e�[�����O�̂���Ɠ����ł������悤�ɓ����Ȃ̂ł��B�܂��A�I���G���e
�[�����O�̎���V�~�����[�g���瓾���鐔��i���}���j�́A�u�p�X�J���̎O
�p�`�v�Ƃ��Ēm���Ă�����̂ŁA�i�q�̑���ɂ�����g���Đ��w�L��6�b4
�̈Ӗ����l���邱�Ƃ��ł���B
�@�U����S�Ƃ�g�����Ƃ́A�S���u�I�ԁv�A�Q�́u�I�Ȃ��v���Ƃ�
�Ӗ�����B����̓I���G���e�[�����O�ł����ƁA�S�̌����_�ʼnE�A�c��Q��
�ō��A�܂��́A�S�̌����_�ō��A�c��Q�ʼnE�̘H���s���Ƃ������ƂƓ���
�ł��B�����Ō����_�͂ǂ��ł����܂��܂���B���̈�A���������E�E����
�l���܂��傤�B�ǎ҂��猩�č��������E�E�ƍs�����Ƃ��A�i�q�܂Ŗ߂炸�p�X
�J���̎O�p�`���g���āA����Ō���ƁA�P�A�P�A�P�A�P�A�T�A15�ƂȂ邱�Ƃ�
������܂��B�܂��A�ǂ��̌����_�ł����܂��܂���E�����E�����Ƃ���ƁA
����́A�P�A�Q�A�R�A�U�A10�A15�ƂȂ�܂��B
�@�������ăp�X�J���̎O�p�`�́A���}�E�̑g�����̐��w�L���ɒu�������Ă���
�����Ƃ��킩��B
�@�@�@�@�@ �@�P 0C0
�@�@�@�@�@�@�P�@�P 1�b0 1�b1
�@�@�@�@�@�P �Q �P 2�b0 2�b1 2�b2
�@�@�@�@�P�@�R �R �P 3�b0 3�b1 3�b2 3�b3
�@�@�P �S�@�U �S �P 4�b0 4�b1 4�b2 4�b3 4�b4
�P �T 10�@10 �T�@�P 5�b0 5�b1 5�b2 5�b3 5�b4 5�b5
�P �U 15 20�@15�@�U�@�P 6�b0 6�b1 6�b2 6�b3 6�b4 6�b5 6�b6
�@��̓����{���̓W�J�́A���ʂȂ�@(���{��)0�A(���{��)1�A(���{��)2�A
�E�E�E�E�E �ƁA���Ɍv�Z���ĂS��̓W�J���͓����邪�A10��Ƃ�18��̂悤
�Ɏ����������Ȃ�Ƒ�ςȌv�Z�ɂȂ�̂ŁA�p�X�J���̎O�p�`�𗘗p������w
���ɂȂ�B����������ł��Ђǂ����̐܂��v�Z������A�p�X�J���̎O�p�`��
��ʉ������A�g����n�br�̌v�Z������̂��悢���ƂɂȂ�B
�@�����ł́A�p�X�J���̎O�p�`�����R�Ɋl���ł��A���z�Ɍ��т��Q�[��
�E����������������߁A�����̊m���� 0.5�̂��̂��̗p�������A�Ⴆ�ΐ�����
�̂R���e�X�g��R���N�C�Y��f�ނɂ����
�@�@�@n�br(1/3)r(2/3)1-r�@�@(�����O�A�P�A�Q�E�E�E)�@�@
�Ƃ�����ʓI�Ȍ`
n�br��r��1-r�@�@(�����O�A�P�A�Q�A�R�A�E�E�E,���{�����P)
�̓��z�̊w�т�g�D�ł��邱�ƂɂȂ�B
�@��ɍl�������z�ŁA���������傫���Ȃ�ƁA�m���̒l�𐳊m�ɋ���
�邱�Ƃ�����ɂȂ�B���ɑ傫�Ȓl�Ɣ��ɏ����Ȓl�̊|���Z�ɂȂ邩���
����B������ǂ��������邩���ۑ�ƂȂ�B�����Ă������������̂����K��
�z�Ȑ���p�邱�Ƃł��邱�Ƃ𖾂炩�ɂ����̂��A�ށE���A�u���A���Ń��v
���X�A����ɃK�E�X�Ƃ������w�҂����ł������B�@�@
�@�܂��A���̓��z�̋Ɍ��������Ƃ��āA�|�A�\�����z���łĂ���B
�@���̂悤�ɁA�ǂ̂悤�ȕς���̊m�����z���A�{���I�ɂ͓��z�̕ό`
�ɂ����Ȃ��Ƃ����邱�Ƃ���A�u���ׂĂ̊m�����z�𗝉����錮�ł���v�ƌ�
������Ɏ��ۓI�ɂ����_�I�ɂ��d�v�Ȋm�����z�Ȃ̂ł���B
���@��
��ہE���ۊԂ̊K�i������~�肷�钊�ێv�l������Ώۂ�
�[�V�w���v�̂̊w�͊ρE���ފς����z���邽�߂Ɂ[
���w�ȊO�̖��ɏo���킵���Ƃ��ɑΏ��ł��鐔�w�����
�@�����{�̓]�@�ł��������a30�N��A�H�ƍ��Z�𑲋Ƃ��Z�p���̎d��������
�������́A�킸���R�N�ő�w�̍H�w�����u�����ƂɂȂ�B���̎��̓]�@�ƂȂ�
���̂́A���{�ōŏ��̃A���~�ԗ��낤�ƈӋC���ޗD�ꂽ�Z�p�҂Ɉ͂܂��
�d�������鎩���̐��w�Ɨ͊w�̗͕s����Ɋ���������ł������B
�@���̍��̐��w����ւ̉ۑ�ӎ��͍��Ȃ��N���Ɋo���Ă���B
�@�����Ɍ����A�u�͂��߂ɐ������肫�ŁA���w���f���������͐��w�I�Ώۂ�
�`�����������ɂ��邠�܂���̓�_�Ō��ׂ�����
�@�@���w�ȊO�̐����Ȋw�I�Ȏ��ۖ��𐔊w������A�Ƃ��������鐔�w��
���p�̋���ɏ\���łȂ�
�@�A��X�ɐ��w�I��i���\���łȂ����߁A�ǂ̂悤�ɂ��Đ��w�I�ɃA�v���[
�@�@�`���Ă悢���킩��Ȃ������ۂɑΏ����鋳��ɏ\���łȂ��v
�Ƃ������̂ł������B
�@�c�O�Ȃ���ƌ����悢�̂��A���R�Ȃ���ƌ����悢�̂��A��w�ł�����
�Ă��炦���A���w�j���͂��߉Ȋw�j�A�Ȋw�Z�p�_������Ɏ~�܂炸�A�F��
�_�ɓN�w�܂Ŏ��L���A���̋�����̉ʂĂ͐��w�����w�Ȃ֓]�Ȃ���������
�Ă��炦�Ȃ������B
�@���ɂ��Ďv���A���E�I�ɁA���w�␔�w���炪���̉ۑ�ɉ�������̂ɂȂ�
�Ă��Ȃ���������A�|���A��m�C�}�����͂��߂Ƃ���A���w�̐���������A��
�̌o���I�����������҂����������̂��낤�B
����ۂƒ��ۊԂ̊K�i������~�肷�钊�ێv�l�̋����
�@�^����ꂽ�ۑ肪�A��ۓI�E�o���I�Ȃ��̂ł���A���ۓI�E���w�I�Ȃ��̂�
����A�܂������ėv�������\�͂́A���ۂƎ̏ۂɂ���āA��̓I�Ȃ��̂�
������A��̓I�Ȏ����̒�����A���ʍ��Ƃ��Đ����ł��邱�Ƃ��܂Ƃ߂�ȂǁA
�l�ԒN�������s���u���ہv���Ƃ����v�l�ƁA���̋t�́A���ی`������̓I�Ȏ�
��Ɍ��т��čl����u��ہv���Ƃ����v�l�̓�̑��ʂ���e�Ƃ���h����
�v�l�h���낤�B
�@�Ƃ��낪�A���҂��ǂ��������ێv�l�ɂ͎�����̉e���ŋ�ۉ��̉ߒ���
�����Ă��邱�Ƃ������A����Ɍg��鋳�t�������܂��A��������Ƃ�邱�Ƃ�
�ł����A���ێv�l�A�Ƃ�킯���ۊT�O���C�̗�������̎���ƌ��т��ċ���
�邱�Ƃ����ɂ���҂������B
�@���̋�ہE���ۊԂ̊K�i�̏���~��Ƃ����m�I������}�������Ă݂�B
�@�@�@�@�@ �� ���@�@�@�@�@�w�@�@�@�@�@��
�@�@�@�@�@ �@�@�@�� ��P������ �� ��Q������
�� �� ��
�@ �o���I�E���ۓI��� �� ���فE���ρE�Ұ�� �� ���w�`���E���
�� �� ��
��Q����ہ� ��P����� ��
�@�@�@�@�@ �@ �� �� �@�E�@�|�@�@��@�� �@�@
���L���ȑz���́A�\�z����͂���ދ����
�@���ێv�l��{�����Ƃ́A�P�ɉ��p�̋��炪����Ȃ��Ƃ��A��w����O�ł͕s
�\�ȋ���Ƃ����ȏ�̉ۑ���܂�ł���悤�Ɏv���B�Ȃ��Ȃ�A�w�ȊO
�̉ۑ���������Ă����\�͂́A�ۑ�ɉ����āA���̊j�S�����𑬂₩�Ɍ������A
�I�m�ɑn�ӁE�H�v���ł���u���ې��v���낤�B�����āA�����ł́A�z����
��́A���邢�́A�����Ƒ傫�ȍ\�z����͂Ƃ��̕\�������߂��邩��ł���B
�@�������ނ̂́A�c���̍����璷�����Ԃ�ʂ��čs���A�����ȋ^��A������
���������čs�����ێv�l�̐ςݏd�˂ɂ������E���y�������ĂȂ����낤�B
�����ێv�l�������Ȃ�����͋���ɒl���Ȃ�
�@���w���f���A�������͐��w�I�Ώۂ̌`�����������ɂ���A�����{�I�A����
���Ă͂ߓI�Ȑ��w�����������ςݏd�˂Ă��A��������������ׂ��ݒ肳�ꂽ
���������\�͂����g�ɂ��Ȃ��B���������Ӗ�����A���ێv�l�������Ȃ���
��͋���ɒl���Ȃ��B�Ӗ�������Ƃ���A�m�C�}���̌����A�o���I����ɗ�
���Ԃ�A�o���I�z�O���Ē��������ۉ��̋���f�ނƂ��Ă̑��݂ł���B
�@�@�@�@
���e�̊T�v
��ہE���ۊԂ̊K�i������~�肷�钊�ێv�l������Ώۂ�
�@�@�@�@�@�@�@�@�@�@�@�@�@�ΐ� �R�ݏ���
�V�w���v�̂̊w�͊ρE���ފς����z���邽�߂�
�@�u���U�v�̐��w��f�ނɂ��Ď�����N�������Ƃ͎��̂S�ł������B
�P�j�ł��Ȃ��q�͂���ɏI�n�����A�ł���q�ɂ͂����x�������A�Ƃ������ʁE
�I�ʑ̐��̌Œ艻������ő��i����u����{�y�����v�����̎w���v�́u���w�v
�A����ւ́u����v�I�ᔻ�Ɋׂ炸�A����������Ȃ����ނÂ�������悤�B
�Q�j���̂��߂ɂ́A�u����ꂪ�悭���ƌĂ�ł�����̂́A�����̟�
�𐰂炵����A�n�ӍH�v���ĂыN�������肷��p�Y���Ɏ��ۂ͂��߂��E�E�B
�����̉Ȋw�E�E�͍��{�I�ɂ̓p�Y���ł����Ȃ����̂ɑ����������
�Ă���E�E���ʁA���퐶���Ɍ����鍢�f������Ƃ�������ނ̖��E�E
�Ȋw�ł���|�p�ł���A���̂悤�Ȗ��ȏ�̂��̂Ɏ��g�ނ��Ƃ͂܂�v
�iƽ�߯āu�z���͂̕����v�j�Ƃ������ɑ�_�Ȑ��w�E�w�K�ς̓]�����K�v�B
�R�j���k�����ɂƂ��Č������E���݊���^����ްсE���ނ��ǂ��̋��ނ��o��
�ɁA�߽�ق̎O�p�`���o�ē��z�ɓ��鐔�w������Ꭶ���A�u�̌n�v�ɂ�����
�炸�A�f�Ђ���o�����Ă��{���I�F���ɓ��蓾�邱�Ƃ��咣�����B
�S�j�����ōł����������̂��A���w����ŁA��ہE���ۊԂ̊K�i������~�肷
��u���ێv�l�v������Ώۂɂ��悤�Ƃ������Ƃł������B
�@�@�@�@�@������ ���@�@�@�@�@�w�@�@�@�@�@�� ������
�@�@�@�@ �� ������ ��P������ �� ��Q������ ������ ��
�� �� �� �� �� ��
�@ �o���I�E���ۓI��� �� ���فE���ρE�Ұ�� �� ���w�`���E���
�� �� �� �� �� ��
�� ������ ��Q����ہ� ��P����� ������ ��
�@�@�@�@�@������ �� �� �@�E �|�@�@�� ������ �@�@
�@���҂����ێv�l���������A������f���ċ�ۉ��̉ߒ����������Ƃ�
�����B���t����O�łȂ��A���ێv�l�A�Ƃ�킯���w�`���E�����C�̗�������
�̎���ƌ��т��ċ������ۉ��i���߁E�|��j�����ɂ���҂������B
�L���ȑz���́A�\�z����͂���ށu���ێv�l�v�̋����
�@�u���鐔�w�I�w�₪�o���I���牓������ɂ�A�܂��Ă��ꂪ�w�����x
���琶�܂ꂽ�z�O�̑������Ԑڂɂ����Ȃ���Q��A��R��̂��̂ɂȂ���
����ƁA���̎��ӂɂ͏d��Ȋ댯���܂Ƃ����B�E�E��x���̒i�K�ɒB����
�ƁA�E�E���̎��Â̕��@�͌���ɗ����Ԃ��āE�E�o���I�z�O���Ȃ菬�Ȃ蒼
�ڂɍĒ������邱�ƁA����ȊO�ɂ͂Ȃ��悤�Ɏv����v�iɲ�݁j
�@���w���f���A�������͐��w�I�Ώۂ̌`�����������ɂ��鐔�w�����������
�ςݏd�˂Ă��A��������������ׂ��ݒ肳�ꂽ���������\�͂����g�ɂ���
���B�Ӗ�������Ƃ���Aɲ�݂̌����A�o���I����ɗ����Ԃ�A�o���I�z�O��
�Ē��������ۉ��̋���f�ނƂ��Ă̑��݂ł���A�ƌ����̂͌����߂��ł���
�����B
�@���w�̖����A�X���I���G���e�[�����O���璊�ۉ��������烂�f���u�i�q�v
�ɋ�ۉ����邱�Ƃɂ���āA�v�l�����炵�A�Ӗ��������Ƃ������݂��
�������B�Ⴆ�A�u�����{���̂S��̓W�J���̊e���̌W���͂ǂ�Ȓl���v
�Ƃ������Ȃ�u�i�q�v�Ƃ��A���̓��͂ǂ��֘A����̂��B�B
�@�����_�ō��ɍs�����Ƃ����A�E�ɍs�����Ƃ����Ƃ��A�e�����_�ł̕������
�}������Ɖ��}���̂悤�ɂȂ�B���{���̎����͎}���ꂷ����Ӗ������
�ŁA�X�^�[�g�O�͂O��A�X�^�[�g���ĂP��A���̌����_��ʉ߂��ĂQ��Ƃ���
�悤�ɂł���B���������Ď��}�̂悤�ɕ\���邱�ƂɂȂ�B
�@�@�@�@�@�@ �P�@ �@�@ �E�E�E(���{��)0
�@�@�@�@�@ �� �� �@�@�@ �E�E�E(���{��)1
�@ �@�� �� �� ���@ �E�E�E(���{��)2
�@�� �� �� �� �� �� �E�E�E(���{��)3
�@�� �� �� �� �� �� �� �� �E�E�E(���{��)4
�@�W�J���͂ǂ��������Ƃ��Ӗ�����̂��낤���B�Q��̓W�J����2�{2�����{��2
��\���}���ꂪ�ǂ������Ӗ����������l����Ε�����B
�@�X�^�[�g���獶���Ɛi�ނƂP�~���~���܂肘2�B�X�^�[�g���獶�E�ƉE��
�Ɛi�ނƂ����Ƃ����B�E�E����2 ���Ӗ�����B���̘a�ł���W�J���́A����
�̂Ƃ��Ɠ������}������̉i�p�x�j���Ӗ����Ă���B
�@�������āA���{���̂S��̓W�J���̊e���̌W�������߂邱�ƂƃI���G���e�[��
���O�̂S�i�ڂ̌����_�ɑ��邷�ׂẲ\���̐�������߂邱�Ƃ͓�������
����A���������āA���}�̂悤�ɁA���̗ݏ�v�Z�̊e���̌W���ƃp�X�J����
�O�p�`�̐��w�I���炭�肪�����ł��邱�Ƃ�������B
�@�@�@�@�@�@(���{��)0���@�@�@ �P �P
�@�@�@�@�@�@(���{��)1���@�@ ���{�� �P �P
�@�@�@�@�@�@(���{��)2�� ��2+2����+��2 �P �Q �P
�@�@�@�@�@�@(���{��)3����3+3��2��+3����2+��3 �P �R �R�@�@�P
�@�@�@�@�@�@�@�@�@���̓W�J�@�@�@�@�@�@�@�@�@�@ �߽�ق̎O�p�`
�@�w�ȊO�̉ۑ���������Ă����\�͂́A�ۑ�ɉ����āA���̊j�S�����𑬂�
���Ɍ������A�I�m�ɑn�ӁE�H�v���ł���u���ې��v���낤�B�����āA������
�́A�z������́A���邢�́A�����Ƒ傫�ȍ\�z����͂Ƃ��̕\�������߂��A��
�����ނ̂́A�c���̍����璷�����Ԃ�ʂ��čs���A�����ȋ^��A�����Ȗ���
�����čs���u���ێv�l�v�̐ςݏd�˂ɂ��n���������ĂȂ��B
���������Ӗ�����A�u���ێv�l�v�������Ȃ�����͋���ɒl���Ȃ��B