さまざまな相を持つ「ハノイの塔」



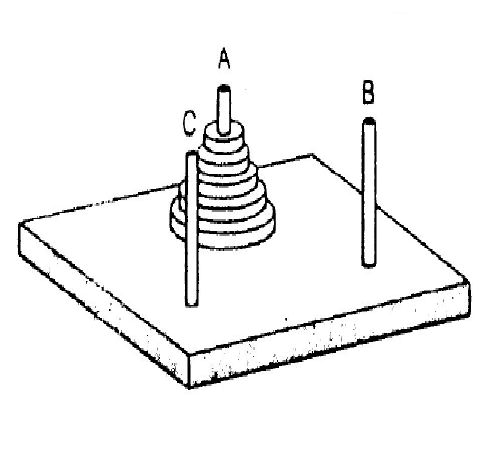
いまでは百円ショップでも売られる子どもの遊具とおぼしき「ハノイの塔」

は、世界のパズラーをはじめ、数学者やコンピュータ科学者、認知心理学者

にとって尽きぬ魅力があるようです。

　以下に書くように、この遊具の遊びを通して、幼児の遊びから始まって、

その遊びの延長上に、数列・差分・漸化式などの数学をはじめ、再帰という

コンピュータ・プログラムに関わる内容の「学び」が構成できます。

　この「遊びを介して数学化し、文字・式などの数学形式の理解と展開」に

至るという認識発達の教育上（教育課程編成原理）の意義については最後に

書いてあります。


1.ゲーム・パズルとしての「ハノイの塔」

　まず、「ハノイの塔」について簡単にご紹介します。

　図のように、三本の柱の一本Ａに大小の円板が、下を大に上が小に順序良

く差し込んである。

 

　

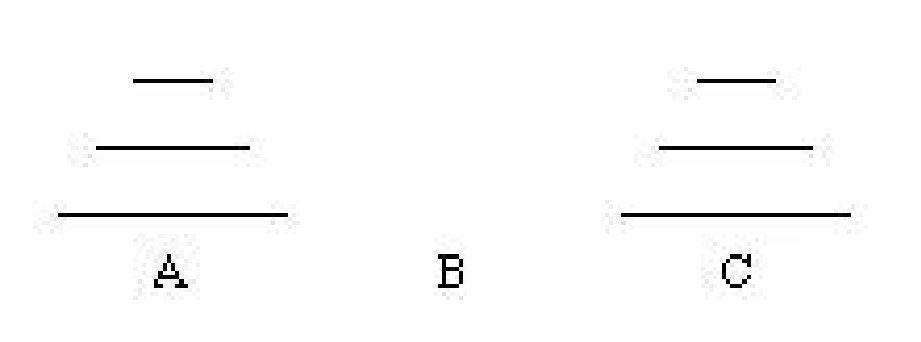
　次のルールを満たして、ＡからＢあるいはＣの柱に移動させる（図の場合

は、Ｃの柱に移動させた）最小の手順を見つけよ、というものです。

　ルール１；円板を１つの場所から別の場所に移しかえるのは１回１枚だ

　　　　　　けでなくてはならない。

　ルール２；移動にあたっては小さい円板の上に大きい円板を置いてはな

　　　　　　らない。

あるいは、ハノイの塔のパズルとはつぎのようにも言える。

上図のように、A、B、C の３本の棒の Aに、中心に穴のあいた大小 n枚の同

じ大きさのない円板が下から大きい順に差してある。一番上の円板は、上記

ルールに沿う限り自由に他の棒（場所）に移動できる。

n枚の円板を Aの棒（場所）から Cの棒（場所）へ移し替えるとき場所

Cに Aと同じ形に移しかえるには何回円板を動かせばよいか。

これをアニメにしたのが、左メニュー「Power Pointによるルール解説」です。

　なお、円板の代わりに大小３種の紙片、柱の代わりに、場所Ａ、Ｂ、Ｃの

三ケ所を紙上に書けば自分で手軽に試みられる。左メニューの「動画による

ルール解説」の学生がアナウンスしているストリーミングがそれです。

閲覧するだけでなく貴方も試みて、作業や問題に答えて下さい

　これは、一昨年、私の講義を受けた学生が、小学生の「学び」用に工夫し

たモノ・教具であり、電子メディアが大きなウエイトを占めることになるで

あろう２１世紀における「教育の創造的研究と革新」を模索する一環として、

「デジタル手法と従来のアナログ教材を適切に融合した学習環境づくり」を

テーマにする講義『コンピュータと教育』において受講生との協同で作成し

たものです。
　ここでは『ハノイの塔』の問題の意味を

　　　家が古くなったので「引っ越し」をする

小さい円板の上に大きい円板を置いてはいけないというルールを

　　　子どもの上にお父さんやお母さんが乗ってはいけない

とか

　　　お母さんの上にお父さんを乗せてはいけない
というように

　　　小さい身体の人の上に、大きな身体の人を乗せてはいけない

と擬人化させています。

この後しばらく、左のメニューに沿って、「ハノイの塔」を学んでいって下さい

問題１；ルールの後半を「次のルールでＢあるいはＣの柱に移動させる

とき、円板の枚数が何枚増えても最小の移動回数で移動できるアルゴリズム

を見つけよ。」と変えると別の問題になる。


問題２； n枚の円板からなるハノイの塔のパズルにおいて、最小移動回

数f(n)を求めよ。

円板の最小移動回数f(n)を求めるさまざまな方法

１）円板を実際動かして移動回数を求める（省略）

２）数列の法則性を見つけ出して求める


　円板の枚数が１枚の時１手、２枚の時３手です。円板の枚数が３、４、

５枚・・・と増えた時、手順はどう増えるだろうか。

　　　枚数｜　１　２　３　４　５　６

　　　ーー＋ーーーーーーーーーーーーーー

　　　手順｜　１　３　？　？　　　　


階差数列

　　　枚数｜　１　 ２ 　３ 　４ 　５ 　６
　
　　　 --- ＋------------------------------

　　　手順｜　１　 ３　 ７　 ？　 ？　　　　　

　　 階差｜　 ２ ４ ６ ？ 



3）解を求めるアルゴリズを再帰的に構成し、それ

をもとに円板の移動回数を求める

　ここで再帰(さいき)とは、もし、与えられた問題よりも規模の小さい問

題が解ければ、その解を用いて、より規模の大きな問題も解けるに違いな

い、というのが再帰の考え方。

　２枚の場合は３手で移動できる。３枚の場合は２枚の場合の結果を２回

利用して、３＋１（３枚目の移動）＋３＝７手で移動でき、４枚の場合は

３枚の結果を使い７＋１＋７＝15手です。以下同様で、次のようになる。

　２枚のとき　３　手

　３枚のとき　３＋１＋３＝７ 手

　４枚のとき　７＋１＋７＝15 手

　　　・・・・・・・・・・・・・

　n枚のとき　an-1＋１＋an-1＝an　・・・・・(1)

となる。

　階差数列の下表から　an‐an-1＝2n-1　・・・・・(2)

が求められる。　

　　 枚数｜　１　 ２ 　３ 　４ 　５ 　６・・・an-1 an

　　　 ---＋----------------------------------

　　 手順｜　１　 ３　 ７　 15　 31 63・・・・　　　　　

階差｜　 ２ ４ 8 16 32 ・・・・２n-1

(1)から　an＋１＋an　＝an＋1　　すなわち　an＋1＝２an＋１・・・・・(3)
同様に、

(2)から　an＋1＝２n＋an・・・・・(4)

(3)、(4)より　2an＋１＝２n＋an したがって　an＝２n−１


nに自然数を代入すると表は再現され、一般項an＝２n−１の正しさが検証

されたことになる。


　 n ｜ １　２ ３ ４ ５ ６・・・

----＋------------------------------

an｜　１　３　７　15　31 63・・・



４）数学的帰納法による証明


n=1のとき,円盤をAからBへ移動させるだけだから1回でできる.これは21-1=1に当てはまる. 

　n=kのとき(k枚の円盤のとき)最小回数2k -1 回でできると仮定すると,n=k+1のとき(k+1枚の円盤のとき) 

1） k枚をすべてCに移動する最小回数は, 2k -1回 

　数列{an}の階差を取ると 2 4 8 16 32 ... となる.これは初項2,公比2の等比数列であるから n≧2のとき n=1のときも成り立つ. 

　　　　よって,an=2n -1 である. 

2） 一番大きな円盤k+1をBに移動する回数は 1回 

3） Cにあるk枚の円盤をBに移動する最小回数は1）と同様に2k-1回 

　よって,k+1枚の円盤は (2k-1)+1+(2k-1) =2(2k-1)+1=2k+1-1 
　　　　　つまり,最小回数2k+1-1 回でできる. 

　　　　 以上より,n枚の円盤をAからBへ移動させる最小回数は2n-1 回である.
 

＜別解＞

n 枚のハノイの塔のパズルについて、最短の手順のとき 1 回目に移動させる

最小の円板はどこへ移動させれぱよいか予想し、それを数学的帰納法で証明する。


　定理 n枚の円板からなるハノイの塔は、2n-1回で完成する。
　

証明　n=1のときは明らか。

　n-１に対しては成立すると仮定する。したがって一番大きい円板はAから

まったく動かさずに、それ以外のn-1枚をAからCへ2n-1-1回で移動させる

ことができる（BとCとりかえて考えている）。
 
このときさらに. 2n-1回目に1番大きい円板をAかうBに移す。ふたたび一

番大きい円板をBからまったく動かさずに、それ以外のn-1 枚をCからBへ

2n-1-１回で移動させることかできる。
　
以上によって２n-1(=2n-1‐1+1+2n-1-1)回で、n枚すべてをBに移動することになる。


5) もっと数学的に解く

　◎ n 枚のハノイの塔のパズルについて,次の問いに答えよ。

　(1) n = 3枚のとき、最短の移動手順を示せ。

　(2) n枚のハノイの塔を最短手順で解く再帰的アルゴリズムを示し、それ

　　 を用いて必度な移動回数を求めよ。(ヒント:n枚の問題の解法アルコリ

ズムを、n-1 枚の問題の解法アルゴリズムを用いて表せ。n＝1 のとき
 
　　 は自明である )

略解　(1)上記２）の解法

　(2) x、y、zはA,B,Cの棒のどれかでお互いに異なる棒を指しているとし、

n 枚の円板をxからyへ移すアルゴリズムをP(n;x,y)と書こう。

　　 P(n;x,y)=「n枚をxからyへ移す」

　　 n=1 の手順はそれ以上分解する必要はない。任意枚数の手順がすべて

n=1 の手順に分解できればよい。実際、Pは次のように再帰的に定義
 
 できるから、任意のnについて分解できる。(このように再帰的に表す

ことができる理由の説明は省略するが、読者は説明を考えられたい。)

　問題の解は、P(n;A,C)である。

　　a. P(1;x,y)=｢1枚をxからyへ移す｣

　　b. P(n;x,y)= P(n-1;x,z) P(1;x,y) P(n-1;z,y) 　n≧2



再帰（recursion）と帰納（induction）

~数学的プロセスの具体例~
　
　パズル「ハノイの塔」の数理を考える中で、階差（差分）と

再帰の考えによる立式と、階差（差分）による推測した式がす

べての自然数について成り立つことを数学的帰納法を用いて調

べてきました。

　実は、再帰と帰納は、どちらも

　　　大きな問題を、同じ形をした小さな問題に帰着させる

という点では本質的に同じです。両者の違いは方向です。つまり、

　　　大きなものからだんだん小さいものへ

というように進むのが再帰的（recursive）な考え方です。一方、

　　　小さなものからだんだん大きいものへ

という方向に進むのが帰納的（inductive）な考え方です。

１）顔見知りでない尋ね人を見つける〜再帰的アルゴリズムの具体例〜

15人の初対面の人が一列に並んで居て、その中の1人だけ「尋ね人」が居ます。
　　
　あなたは、この人たちに「尋ね人はどこですか？」と質問して、人探しをしなけれ

ばなりません。

　ある人を一人選んで「尋ね人はどこですか？」と質問したとき、以下の3通りの答えのうち、

どれか1つが正しく返ってくるとします。

　　（1）「尋ね人はわたしです」（質問した相手が尋ね人だった場合）

　　（2）「尋ね人はわたしよりも左にいます」

　　（3）「尋ね人はわたしよりも右にいます」

　　この聞き方を下記３人にして尋ね人を見つけることを試みてみることにしよう。

 |  | 

　　この場合、最小回数の質問で尋ね人を探しだすのは簡単で、真ん中の男の人に「尋ね人は貴男ですか？」と尋ねれば

　 （1）当人だったら確定です
　　(2) 私の左に居る人です。
(3) 私の右に居る人です。
と１回で確定できる。
これを１５人の場合に拡張することを考えよう。
１５人の真ん中の人に尋ねると応えは
　　（1）尋ね人だったら確定
　　（2）真ん中の人でなかったら「尋ね人はわたしよりも左にいます」
　　（3）あるいは「尋ね人はわたしよりも右にいます」
と７人、尋ねられた人、７人の３グループに分かれることになる。（この項未完につき編集継続）
２）逆さ「ハノイの塔」

〜認知心理学的に「ハノイの塔」を見ると〜

　逆さ「ハノイの塔」を説明します。

　 


　　逆さ「ハノイの塔」は、上図「ハノイの塔」とは大きく違っていて、一番大き

　　い円板が上で、小さいのが下に積み上がっている。つまり、順番が「逆さ」で

　　ある。

　　また、問題もルールもつぎのように違う。

　＜問題＞は、三つの深皿を最初にあった場所から一つの場所に一つの深皿が左か

　　ら右に大、中、小の順になれば終わりとした。円板（紙片）では見えなくなる

　　ので折り紙で大中小３つの深皿を折って使用した。

　　ルール１；一度に移せるのは、一つの深皿だけ。

　　ルール２；深皿が移せるのは、移した結果その深皿がその場所に最大の深皿に

　　　　　　　なる場合に限る。

　　ルール３；場所に置かれた深皿のうち、最大のものだけを他の場所に移せる。　

　実は、この＜問題＞を板と深皿の両方で行った場合、難しさの点で大きく違って

くる。円板（紙片）の場合は深皿のおよそ2.5倍時間がかかり、およそ２ 倍動かし、

エラーは６倍にもなるという。形状が影響しているという。

　教師が、教材・教具を工夫するときに考えなければならないことを教えられる。

　　（ノーマン『人を賢くする道具〜ソフトテクノロジーの心理学』新曜社より）

Spiral Curriculumと『基礎・基本』、そして講義『ハノイの塔』のねらい

表象構造と認識

　 Spiral Curriculum は螺旋型的に上昇過程をたどる形態をもった教育課程

を意味している。
 
この教育課程は、基本的にはブルーナー(Bruner,J.S.)が提起した子どもの

表象構造の発達

	運動的表象　→　映像的表象　→　記号的表象


を根拠にして成立した。運動的表象による認識段階にある子どもが、ある対

象物を運動的表象によって認識した場合、子どもが発達段階の経過とともに

表象構造を変革しながら、同一の対象物を映像的表象、さらには記号的表象

によって認識するならば、その認識はより明確でより精確なものとなる。

これが Spiral Curriculum の基本原理です。



認識論理の同一性と教育への適用

　そこでは、それぞれの発達段階にある子どもの固有の表象構造に適合した

教材を計画的に準備、配列し、次の発達段階では、その段階での表象構造に

変容された同一の教材を教育内容として設定するという教育課程編成方針が

とられることになる。また、この教育課程理論では、各発達段階における子

どもの認識の表象構造は異なるにせよ、そこでの認識の論理は同一、共通で

あるという見解がとられ、知的活動の論理は、科学研究の最前線でも小学校

３年生の教室でも同一であると主張したブルーナーが有名。この二つの違い

は「程度(degree)」の事柄であって「質(kind)」の問題ではないといわれる。

ここから科学的認識の思考・論理と学習者の学習・認識の論理の同一性と

いう結論が導出される。
 
 教材論としては、この認識の論理の同一性を根拠にして、教材をそれぞれ

の発達段階にある子どもの固有の表象構造に「翻案する(translation)」とい

う論理が主張されることになる。(日本カリキュラム学会編『現代カリキュ

ラム事典』'01.2)

お詫び：ビデオ中で「ブルーナー」のことを「ブルーム」と言い間違えています。お詫びし、訂正します

日本の教育課程編成原理としてのスパイラル方式の実態と欠陥
 日本の教育課程編成原理は、このスパイラル方式だが、その一面である発
達段階重視に偏りすぎる。この傾向は、「積み上げが大切で、基礎が育って
いなければ分らなくなるのは当然」という風潮や生物発達的限界説を唱えた
りする欠陥がある。教育過程の構成にあたっては教材を構成しなければいけ
ないのだから当然のことながら構成的でもある。しかし、その実態をつぶさ
に見ると、そこにはブルーナーの三段階構成を踏まえた教材構成になってい
るとは言い難い。
　今ばやりの「基礎・基本」という視点から教材構成を見ると、教材の構成
上、何が「基礎」になっていて、どの教材がその全教材にとって「基本」な
のかが定かでない構成になっていることが多く、この指導要領に準拠した教
科書の構成は、今も昔と変わらず、「基礎・基本」とは実体定かでない「い
ずれは役に立つ」、あるいは「今後の展開で必要な下部概念に位置する」程
度にしか捉えられていないと思われる。
　こうした構造を分析・批判しているのは、須田勝彦（「中学校数学カリキュ
ラム再構成への試み」北大教育学部教育方法研究室『教授学の探求』第17号
2000.3）である。そこでは面積や割合、乗法などを挙げているが、寺岡英男
（福井大学教育地域科学部）は、日本科学者会議福井支部における講演『学
力問題再考』において面積の扱いを次のように紹介している。

　たとえば前回学習指導要領では、4 年で「面積概念について理解し、
簡単な場合について面積を求めることができるようにする」とある。
「簡単な場合」とは正方形と長方形だけで、教科書では「複雑な面積の
求め方」として、長方形2 個に分割可能な形などが扱われる。そして5
年で「基本的な平面図形の面積が計算で求められることの理解を深め、
面積を求める能力を伸ばす」として、三角形、平行四辺形、台形などの
面積の求め方を学ぶ。こうした扱いは現行学習指導要領になっても基本
的には変ってはいない。
　これに対置する須田たちのカリキュラム構想では、4 年生の面積指導
の目標は「多角形の面積」の完全理解におかれる。その構成は、(1) ２
つの多角形の面積が等しいとは、二つの多角形が有限個の互いに合同な
図形に分割できる（「たちあわせ」の原理）、(2) 任意の長方形は、任
意の長さを一辺とする長方形にたちあわせることができる、(3) 三角形
は長方形にたちあわせることができる、(4) 任意の多角形は三角形に分
割可能だから、任意の長さを一辺とする長方形にたちあわせることがで
きる、(5) 多角形の面積は、長方形の面積論に帰着される、(6) 長方形
の面積は複比例構造をもつ、(7) したがって面積の単位は、長さの単位
を一辺とする正方形を選ぶことが合理的である、などの「基礎的な概念
や原理・法則である」。
　学習指導要領と須田の違いは明瞭である。学習指導要領では簡単な場
合からより複雑な面積の求め方へと段階的に積み上げていく方法が採ら
れている。多角形の面積の「完全な理解」はいつまでも実現されない。
4 年生では長方形、正方形の面積測度の求め方だけが指導される。なぜ
長方形や正方形について考えるのかは示されない。５年生では、平行四
辺形と三角形だけが「たちあわせ」の対象となり、面積の「公式」が示
される。台形は考えない。まして多角形の面積など考えない」。スパイ
ラルなカリキュラムの構成という実態はこの程度のものである。図形の
面積という同一のジャンルに括られる教材が、4年・5年と分散して配列
されているだけで、そうした教材が担っている教育内容（たちあわせの
原理をふまえて「多角形の面積は、長方形の面積論に帰着される」とい
うこと）が、新しい別の内容のなかで、新たな概念との新しい関係を成
立たせたり、新しいはたらきを示したりするわけではない。
　一方、須田の場合には、典型的な実例からの一挙の一般化と、それを
有効に適用する応用という、一般から特殊へという水道方式と同じカリ
キュラムの構成原理がもとになっている。面積の場合、「たちあわせ」
の原理が多角形の面積の「完全な理解」を実現するための武器となる。
このような多角形の面積は、次に曲線に囲まれた図形の面積へ、さらに
は多角形の体積と多角形の面積との異同、一般的な面積や体積とは何か
という、より高次の課題への飛躍が用意される。須田はいう、「基礎的
な概念や原理・法則は基礎的であることによって、自ら螺旋的にくりか
えし、発展するが、恣意的にバラバラに分散することはそのよさのすべ
てを破壊する」と。

講義『ハノイの塔』の構成主義的スパイラル学習方式
 私は、本稿『教育教材としてのハノイの塔』において、二つの意図をもっ
て書いている。
 ひとつは、子どもの表象構造の発達
 
 　運動的表象　→　映像的表象　→　記号的表象

三段階説を適切に使うことによって、人間の系統発生的な認識過程と個々
の子どもの個体発生的認識過程を融合した「教え＝学び」のスタイルを実
現する教材構成の原理・原則が見えること。いまひとつは、この教材構成
によって現代版「教育の現代化」のあり方が見えることをである。
　(詳しくは左メニューの「私流『数学教育論』」参照)

「ハノイの塔」余話


そもそも「ハノイの塔」とはつぎのように投げかけられたパズルでした．
　インドの伝説によれば，ベナレス（現ワーラナシー，ヒンドゥー教の最大の聖地のひとつ）には世界の中央を指示する大寺院が
あった．そこの塔の下に３本のダイアモンドの柱があって，左の柱には天地創造のときに神が穴のあいた６４枚の純金製の円盤を
つきさした．円盤は上にあるものほど半径は小さくなっていた．そして神は僧侶達に休む暇なく，円盤を次の規則に従って移動さ
せ，すべての円盤を右の柱に移すように命じた．
従って，Ａ64＝２64−１
264は20桁の数ですが，ついでですからもう少し正確に求めておきましょう．
264＝18446744073709551615なので，
18446744073709551615秒＞307445734561825860分＞
5124095576030431時間＞213503982334601日＞584554529390年
5845億5452万9390年と言う年月を要します．これならば仮に伝説が正しくてもまったく心配ないでしょう．

＜指数関数・対数関数利用による　264-1　の計算＞
　264-1を計算すればよい.概数が分かればいいのだからきっちり計算する必要はない.こんなとき,対数をうまく利用すれば
難なく計算できる. 
S=264と置こう.両辺の常用対数を取ると, 
logS=log264 =64log 2 
logS≒64×0.301 （　∵　log 2≒0.3010 ）
　　≒19.264 
S≒1.84×1019 （　∵　0.264≒log 1.84 ）
　　∴ 264-1≒1.84×1019 (秒) 
これはどれ位の長さのだろうか.年に直すと約5800億年になる.では世界の破滅は当分来そうにもない.
と安心はしてもいられないのです．以下，世界大百科事典からの抜粋です．
　現在，太陽では４個の陽子から１個のヘリウム核を作る反応が起こっているが，粒子の個数が1/4に減ることによって，中心核
の圧力が減る傾向が生じている．中心核が押しつぶされないように，太陽は温度を上昇させることによって，圧力の減少を自動的
に防ぐ．このためエネルギーの発生量は増加し，太陽はしだいに明るくなり，また膨張していく．計算によると100億年後には明
るさは現在の２倍に，半径は1.4倍に増すはずである．（注．現在は45億年経過）
　この時点で今まで燃えていた水素が中心部からまずなくなり，もえかすのヘリウムが次第に中心部にたまってきて，原子炉は球
殻状の層をなして，次々とより上層の水素を食っていくこととなる．この段階に入ると太陽は急速に大きくなり，明るさは現在の
500倍に，半径は100倍にもなる．ただし表面温度は下がって赤い星となる．赤色巨星である．やき尽くされてどろどろになった
地球から見ると，赤い太陽が空を覆わんばかりの大きさで輝いているであろう．ここまでくると，今までの燃料であった水素はまっ
たく底をついて，もえかすのヘリウムが内部を満たす．燃料切れになった太陽の内部はどんどん重力で収縮し，その結果温度が上
昇する．温度が１億Ｋに達すると今度はヘリウムに火がつく．この反応は激しく爆発的であり，太陽はおそらくその何割かの質量
を失うことになる．身軽になった太陽の中心は適当に冷えて，しばらくはヘリウムが穏やかに燃える．しかしやがてヘリウムも底
をつき，次の燃料に火がつくというようなことを重ねて，これまでと同じくらい激しいいくつかの変動を経て多量の物質を消耗し
て惑星状星雲になり，白色矮星(わいせい)となる．質量は現在の半分に，半径は1/100に減り，原子エネルギーはすっかりなくな
り，高温のために白く輝くがその明るさは1/1000くらいにすぎない．太陽はやがて光を失った小さな天体となってその生涯を閉
じるであろう．


教育における三位一体について
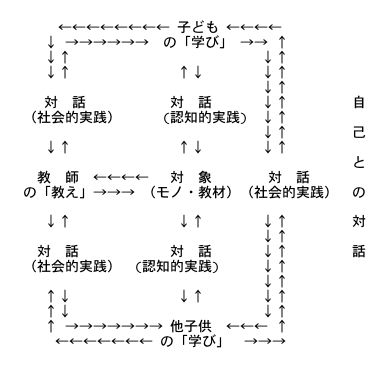
 　教育は、当然のことながら、子ども・教材・教師の三位一体で成立する。
 このことは多くの識者が言及している。
 　例えば、佐藤学は、「学ぶ」という行為を分析し、対象（モノや教材）と
 の対話（認知的実践）を媒介に、他者（他の生徒や教師）との対話（社会的
 実践）、自己との対話（倫理的実践）という二つの“対話的”実践によって
 成立している、と言い、教師の「教え」という行為は、「学び」におけるこ
 の二つの対話的実践を触発し援助し組織する活動である、と。
　私は、担当する講義すべてで、教材は違えても、まず最初に、この相互関
係を下記の図で示し、教育における対象（モノ・教材）の働きの重要性につ
いて、具体的教材で体感してもらうことにしている。