１年生監督対決、落合 vs 伊東のどちらが「日本一」を制するか？！
 
−プロ野球日本シリーズを「数学する」−

１．パスカルの三角形という数学ツール

　　　　　　　　　　　　1　 　・・・・・・・・・・・・0    
　　　　　　　　　　　1 　1　　・・・・・・・・・・・ 1
　　　　　　　　　　 1　2　1　　・・・・・・・・・・  2
　　　　　　　　　 1    3   3　1　　・・・・・・・・・・3
　　　　　　　　  1　4　6　4　 1　　・・・・・・・・・4
　　　　　　　　1  5  10 10　5 　1
　　　　　　　1　6  15 20  15　6　 1

　上左の三角形状に並んでいる数の列は、「パスカルの三角形」と言われている。
　右端に書いてあるのは０段目、1段目、2段目、・・・・を示す。7段目がどのよう
な数列になるかお分かりだろうか。また、８段目、９段目、10段目と数値を入れて自
作して頂きたい。（書き込み用紙印刷）
   自作してここをクリックすれば正解が見られます。

　このパスカルの三角形がプロ野球日本シリーズを「数学する」ことに挑戦できる数
学ツールなのです。

２．パスカルの三角形と勝敗分析の山岸の四角形
　ドラゴンズとライオンズが実力伯仲しているとして７戦戦い、どちらかが４戦先勝
で勝ちとなり、これ以上の試合は行わない。
　ここのところがパスカルの三角形と比較したとき違うところであり、パスカルの三
角形の左下と右下の隅はいらなくなった下図のような四角形で考えれば良い。
　下図右の勝敗表は、毎日の試合によって起こりうるすべての状況を表わしている。

　　　　　　　　 可能性ある試合数　　　　可能性ある勝敗表
　　　　　　

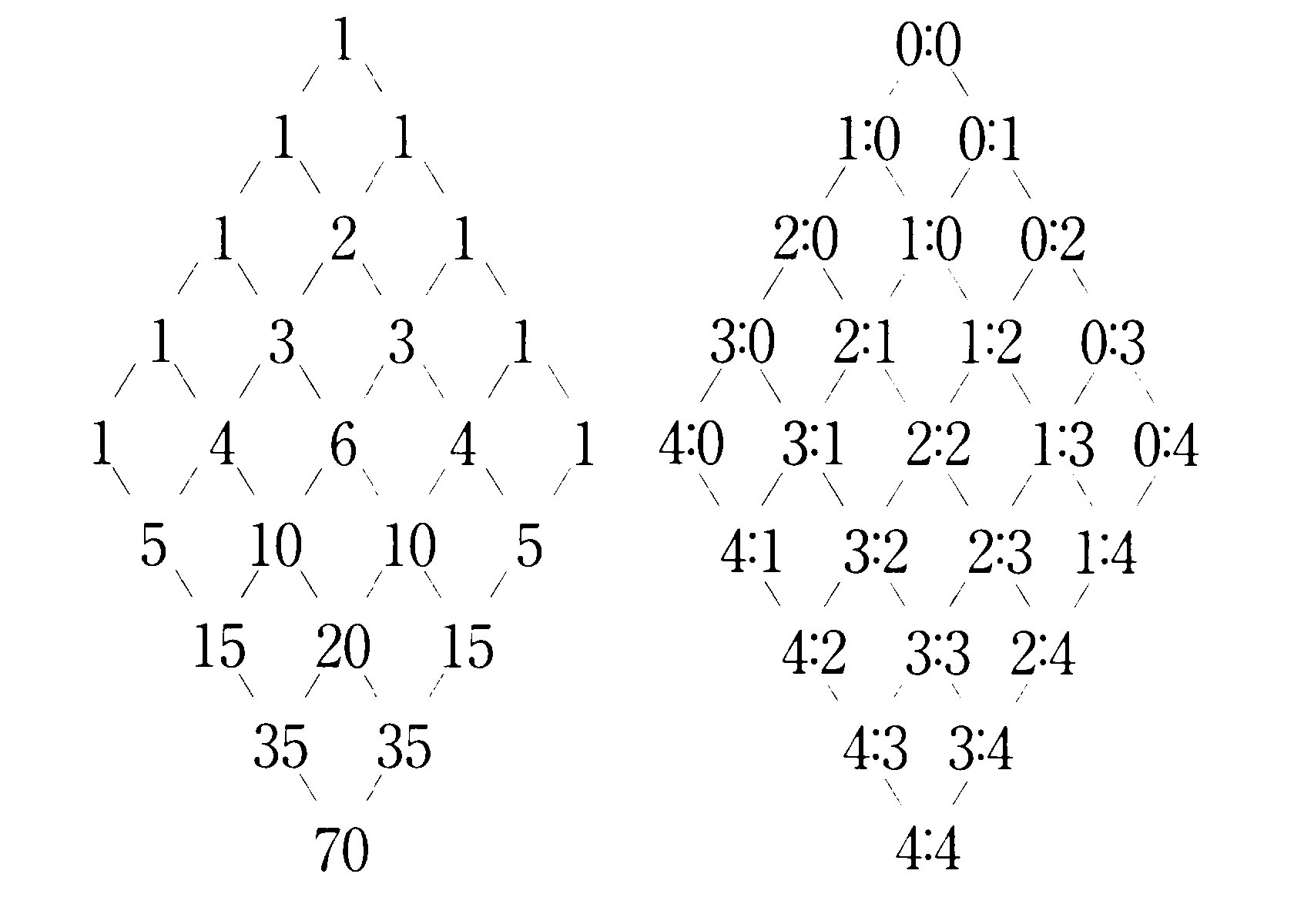　勝敗表最上段の(0：0)とは、ドラゴンズもライオンズも1勝もしていない試合前の
状態を示したもので、両方が４勝した(４：４)は、どちらかが勝って優勝してしまっ
て実際には起こりえない架空の試合を意味し、参考に書いたものにすぎません。

３．プロ野球「日本シリーズ」の確率計算　　
　毎日の試合で起こりうる勝敗を書き上げたのが上右図。今夜の第１戦においてドラ
ゴンズが勝てば、ライオンズ対ドラゴンズの対戦を（ライオンズ：ドラゴンズ）と書
くと、 (0:0)点から(0:1)点を辿り、ライオンズが勝てば、 (0:0)点から(1:0)点を辿
ることになる。その可能性として、共に(4:3)、(3:4)まで勝敗の経過があるとすると
全経過70通りあることになります。
　どちらかが４勝すればシリーズは終わるので、(４：２)や(３：４)など一方が４の
勝敗はそこで日本シリーズは終了を意味します。
　それぞれ松坂と川上の豪腕投手を擁する豊富な投手陣の両チーム、打線は、豪打の
ライオンズと堅実な打撃陣のドラゴンズと力量は互角（1/2:1/2）として、試合前の
勝敗可能性のを計算したのが次表の確率計算です。

　　　　　可能性の確率計算　(L、Dはライオンズ、ドラゴンズの略記。以下同様)
　　　
　　　　　L　  　 １　　　D
　　 　　　　1/2 　1/2                 
　　　　 1/4 　 2/4 　 1/4 　　　　
　　　1/8　  3/8　 3/8    1/8　　　
　 1/16  4/16  6/16   4/16 1/16　
　　  4/32  10/32 10/32 4/32　　
　　　　 10/64  20/64 10/64　　　
　　　　　 20/128 20/128 　　　　
  　　　　　　　                 　　　　
　勝敗の一方が４の最終結果を表す勝敗表に対応する確率計算は注意を要します。そ
の確率、例えば、(４：２)で勝負がつく場合の確率計算はパスカルの三角形を鵜呑み
に機械的に計算すれば１５/６４になることになりますが、日本シリーズの確率計算
では10/64としなければなりません。なぜなら、その確率計算では、どちらかのチー
ムが４回勝てばシリーズが終わってしまうので、(４：０)で勝負がつく１通りと(４：
１)で勝負がつく４通りの計５通りの場合を勘定に入れてはならないので分子が５少
なくなって10/64になるわけです。同様に、最終結果を表す右下と左下の確率の分
子は、パスカルの三角形の対応する場所に書かれる確率の分子とは違ってくる。
また、左下の総和（1/16＋4/32＋10/64＋20/128＝64/128＝1/2）はライオン
ズの優勝確率、同様に、右下はドラゴンズの優勝確率、その和つまり１は、どちらか
が優勝することを意味します。
　これでプロ野球日本シリーズの確率計算の枠組みはできたことになります。しかし、
この計算は第１試合がはじまる前までしか通用しないもので、第１戦の勝敗が決まる
とまた違った計算をしなければならなくなることになります。
既述の通り、第１戦でドラゴンズが勝てば、ライオンズ対ドラゴンズの対戦を（ライ
オンズ：ドラゴンズ）と書いているのですから、 (0:0)点から(0:1)点を辿り、第２戦
目は、(0:1)のところを初戦に以降の可能性の確率計算をすればよいことになります。
ライオンズが勝てば、 (1:0)のところを初戦に以降の可能性の確率計算をすればよい。
　問題　１）第１戦の結果から、第２戦試合前に２戦以後の可能性の確率計算を行え。
　　　　　　ただし、両軍の力は互角と仮定する。
　　　　２）第１戦が勝った場合の両軍の優勝する確率計算を行い、第１戦を勝った
　　　　　　チームが優勝にどれほど優位になったかを計算せよ。
計算用紙を印刷してお使い下さい。