● 連載● 子どもが(数学する)授業 迷 子 の ペ ッ ト を 探 せ !? 〜仲間あつめ、二進法、そしてコンピュータまで〜 豊かなアイデアにたどり着くのに必要なのは美的直観である. 美的直観とは、これまでは無関係と思われていたものの間に関係が あることを発見すること アンリ・ポアンカレ [1] 迷子のペット探し?! 1) あなたのペット当てます 8 匹のペットのイラストが掲載された紙を計4枚見せます。どれか1枚で どれか1匹のペットを覚えてもらった上で、それぞれの紙を見てもらい、同 じペットがいるか答えてもらう。その覚えてもらったペットを私が当てます。 なぜ私が当てることができたかを明らかにしつつ、併せて、一見無関係と 思われる小・中・高・大の教材の間にある関連性に注目させる実践です。 2) 迷子のペット探し お年寄りたちが可愛がっていたペット1匹が行方知れずになった。そのペッ トの次のような特徴をお年寄りから聞いた(以下、目撃情報)。 ・大人しく誰にでもすぐなつく ・鼻の頭が黒い ・首輪をしていた ・真っ白でない ペットのイラストは下の写真です。迷子のペットはどのペットでしょうか?
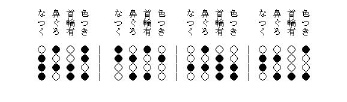 今、4つの白丸○の代わりに、4つの穴を空けた一組16枚のカードを渡し黒
丸にあたる部分を上から切り欠く(Uとする)と、先の例のペットならU〇U○
となる。このカードに対応する絵を切り離し貼付ける。同じように、全カード
に切り欠きを入れ、それぞれと対応する絵を貼る。なお、カ―ドに切落し部を
つけ方向づけしておく。
今、4つの白丸○の代わりに、4つの穴を空けた一組16枚のカードを渡し黒
丸にあたる部分を上から切り欠く(Uとする)と、先の例のペットならU〇U○
となる。このカードに対応する絵を切り離し貼付ける。同じように、全カード
に切り欠きを入れ、それぞれと対応する絵を貼る。なお、カ―ドに切落し部を
つけ方向づけしておく。
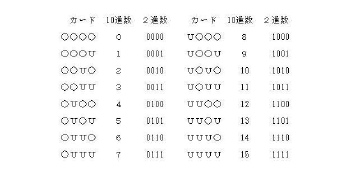 込んで順に並び替わったカードの10進数を見ると小から大の順に並らんでいる
ことが分かる。
この操作をデータの並び替え(ソート)といいます。
サーチとソートは、コンピュータの基本動作です。こうした意味から、このカ
ードを「簡易コンピュータ」と呼んでいます。ノイマン型コンピュータはこれに
"記憶"装置を備えていると。
[3]"ペット当てマジック"の数学的「謎解き」
最後に最初の"ペット当てマジック"の種明かしです。
4枚の紙のペットの裏には上記2進法の法則に則った10進数を書き込んであ
り、同じペットがいると答えてくれた場合、つぎに解説するように、紙の裏面の最
小の数字をすべて足すと、どのペットを選んだかが分かる仕組みになっている。
紙幅の都合で、ペットカード3枚(10進数1〜7)の場合で説明する。
1枚目の数字(絵) 1、3、5、7 2進数1桁目が1の集合である
2枚目の数字(絵) 2、3、6、7 2進数2桁目が1の集合である
3枚目の数字(絵) 4、5、6、7 2進数3桁目が1の集合である
覚えてもらった 1 = 00001 2進数計算にすると
数字が3枚とも カードの最小数の計算 2 = 00010 左の縦加算をすると
あったと答えた 4 = 00100 00111
つまり、答えは10進数の 7
覚えてもらっ 1 = 00001 2進数計算にすると
た数字が2枚 カードの最小数の計算 4 = 00100 左の縦加算をすると
目になかった 00101
つまり、答えは10進数の 5
覚えてもらっ 2進数に直すと
た数字が3枚 カードの最小数の計算 4 = 00100 00100
目だけあった つまり、答えは10進数の 4
[4]数学で「科学」を教えるとはなんだろうか
"数学"の学びの楽しみのひとつに、冒頭引用のポアンカレの言う、全く異なる
幾つもの事象の間に、思いがけない同一パターンを見出すことがある。このことの
意義は、教育においても同様で、ホワイトヘッドは、教科書の単元の恣意性を綿密
に批判し、学びは本来、単元間のつながりを学んだり、関連性を見つけることであ
るとし、「関連性の探求を省略するいかなる学問体系も科学的たり得ない」(『教育の
目的』)といった。翻って、指導要領や教科書を見ると、関連ある教材にも拘らず別
の単元で関連なく教えられ、ホワイトヘッドのいう意味で"科学"を教えるものに
なっているとは言い難い。AMI実践でも同様の傾向に陥っていないだろうか。
本稿の教材 "迷子のペット探し"は、私の大学講義 『教科・算数基礎』 の講義
内容の一部を、学生が自分の理解確認のために自作したものを使わせていただいた。
講義全般は、小学新入生の算数の冒頭教材「仲間あつめ(集合数づくり)」から記数
法とその一つ2進法 ・ 2進数、アルゴリズムの基本(サーチとソート)、ハノイの
塔、数 ・ 文字計算の計算体系づくりなど、小・中・高・大に跨る一見無関係と思わ
れる教材の間の関連性に注目させることをテーマにしている。学生たちは、2進数に
よるペットの集合づくりが小学新入生の集合づくりの拡張であることや、中・高生で
学ばされた浅薄な2進数計算と異なる広い視野のBinary Worldに興味を示す。
小・中・高教材の再考に資することもできるのではないだろうか。
込んで順に並び替わったカードの10進数を見ると小から大の順に並らんでいる
ことが分かる。
この操作をデータの並び替え(ソート)といいます。
サーチとソートは、コンピュータの基本動作です。こうした意味から、このカ
ードを「簡易コンピュータ」と呼んでいます。ノイマン型コンピュータはこれに
"記憶"装置を備えていると。
[3]"ペット当てマジック"の数学的「謎解き」
最後に最初の"ペット当てマジック"の種明かしです。
4枚の紙のペットの裏には上記2進法の法則に則った10進数を書き込んであ
り、同じペットがいると答えてくれた場合、つぎに解説するように、紙の裏面の最
小の数字をすべて足すと、どのペットを選んだかが分かる仕組みになっている。
紙幅の都合で、ペットカード3枚(10進数1〜7)の場合で説明する。
1枚目の数字(絵) 1、3、5、7 2進数1桁目が1の集合である
2枚目の数字(絵) 2、3、6、7 2進数2桁目が1の集合である
3枚目の数字(絵) 4、5、6、7 2進数3桁目が1の集合である
覚えてもらった 1 = 00001 2進数計算にすると
数字が3枚とも カードの最小数の計算 2 = 00010 左の縦加算をすると
あったと答えた 4 = 00100 00111
つまり、答えは10進数の 7
覚えてもらっ 1 = 00001 2進数計算にすると
た数字が2枚 カードの最小数の計算 4 = 00100 左の縦加算をすると
目になかった 00101
つまり、答えは10進数の 5
覚えてもらっ 2進数に直すと
た数字が3枚 カードの最小数の計算 4 = 00100 00100
目だけあった つまり、答えは10進数の 4
[4]数学で「科学」を教えるとはなんだろうか
"数学"の学びの楽しみのひとつに、冒頭引用のポアンカレの言う、全く異なる
幾つもの事象の間に、思いがけない同一パターンを見出すことがある。このことの
意義は、教育においても同様で、ホワイトヘッドは、教科書の単元の恣意性を綿密
に批判し、学びは本来、単元間のつながりを学んだり、関連性を見つけることであ
るとし、「関連性の探求を省略するいかなる学問体系も科学的たり得ない」(『教育の
目的』)といった。翻って、指導要領や教科書を見ると、関連ある教材にも拘らず別
の単元で関連なく教えられ、ホワイトヘッドのいう意味で"科学"を教えるものに
なっているとは言い難い。AMI実践でも同様の傾向に陥っていないだろうか。
本稿の教材 "迷子のペット探し"は、私の大学講義 『教科・算数基礎』 の講義
内容の一部を、学生が自分の理解確認のために自作したものを使わせていただいた。
講義全般は、小学新入生の算数の冒頭教材「仲間あつめ(集合数づくり)」から記数
法とその一つ2進法 ・ 2進数、アルゴリズムの基本(サーチとソート)、ハノイの
塔、数 ・ 文字計算の計算体系づくりなど、小・中・高・大に跨る一見無関係と思わ
れる教材の間の関連性に注目させることをテーマにしている。学生たちは、2進数に
よるペットの集合づくりが小学新入生の集合づくりの拡張であることや、中・高生で
学ばされた浅薄な2進数計算と異なる広い視野のBinary Worldに興味を示す。
小・中・高教材の再考に資することもできるのではないだろうか。